Gas Laws
Ideal Gas Law
The definition of the ideal gas:
- Atoms and molecules are
idealized as mathematical points (their volume is neglected compared to
the total volume of the gas)
- All collisions between atoms or
molecules are perfectly elastic
- There are no intermolecular
attractive forces
The equilibrium states of a simple, compressible substance can be specified in terms of its pressure (P), volume (v) and temperature (T). If any two of these state variables is specified, the third is determined. This implies that the states of the substance can be represented as a surface in a three dimensional PvT space.
The ideal gas law
Pv = n RT
P: pressure = force / surface: 1 Pa = 1 N /
(101.325 kPa = 1 atm)
v: volume
m3
n: mol = m / M
m:
mass g
M:
molar mass g/mol
R:
constant = 8.3143 J / mol K
T: temperature en Kelvin, 0ºC = 273.1 K Kelvin temperature scale
The ideal gas law is generally valid at low pressure, large volume and high temperature.
All the
possible states of an ideal gas can be represented by a PvT surface as
illustrated below. The behavior when any one of the three state variables is
held constant is also shown. Pi, vi, and Ti
are the Pf, vf, and Tf are the final values.
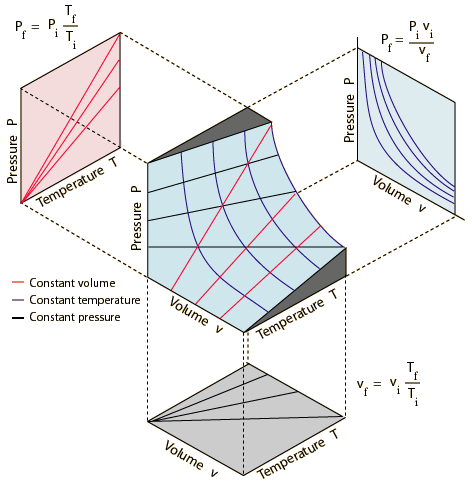
See details in:
http://hyperphysics.phy-astr.gsu.edu/hbase/kinetic/idegas.html
Real Gases
The Ideal Gas Law is invalid:
At low temperature,
high pressure, and small volume
van der Waals Equation of State
The ideal gas law treats
the molecules of a gas as point particles with perfectly elastic collisions.
This works well for gases in many experimental circumstances (low P, large v,
high T). But gas molecules are not point masses, and there are circumstances
(high P, small v, low T) where the properties of the molecules have an
experimentally measurable effect. A modification of the ideal gas law was
proposed by Johannes D. van Waals in 1873 to take into account molecular volume
and molecular interaction forces. It is usually referred to as the van der
Waals equation of state:
[p + a (n/V)2] [V – n b] = n RT (1)
where nb is approximately the volume occupied by the molecules themselves,
The pressure can be expressed as: p = nRT / [V – n b] - a (n/V)2
The pressure
exerted by the gas on the walls of the container is related to the number and
frequency of the collisions with the wall. These are both reduced by attractive
forces between the molecules and this is included in the -a(n/V)2 term.
The numeric values of the constants a and b are
determined experimentally.
Table 1: Constants de van der Waals
|
gas |
a [dm6 atm / mol2] |
b [dm3 / mol] |
|
ammonia (NH3) |
4,170 |
0,0371 |
|
nitrogen (N2) |
1,345 |
0,0391 |
|
Carbon dioxide (CO2) |
3,64 |
0,0427 |
|
Methane (CH4) |
2,283 |
0,0428 |
Another units:
|
van der Waals Coefficients |
||
|
Gas |
a (Pa m6/mol2) |
b(m3/mol) |
|
Helium |
3.46 x 10-3 |
23.71 x 10-6 |
|
Neon |
2.12 x 10-2 |
17.10 x 10-6 |
|
Hydrogen |
2.45 x 10-2 |
26.61 x 10-6 |
|
Carbon dioxide |
3.96 x 10-1 |
42.69 x 10-6 |
|
Water vapor |
5.47 x 10-1 |
30.52 x 10-6 |
Data from Fishbane, et al.
Gaseous Equation of State Calculator
Home work
assignment: Calculate and draw the van der Waals p-V curves for a given gas at
300 and 400 K (use Excel).