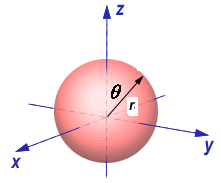
y = r sin(q) sin(f),
z = r cos(q).
Les orbitales hidrogenoides: Z=1
Les coordonnées spheriques:
 |
x = r sin(q) cos(f), y = r sin(q) sin(f), z = r cos(q). |
Y(r,q,f) = Rn,l(r).Yl,m(q,f)
Partie radiale: Rn,l(r),
Partie angulaire: Yl,m(q,f)
L'unité de distance atomique: a0 = 52.918 pm.
|
no. quantiques |
O.A. |
Rn,l(r) |
Yl,m(q,f) réelle |
Complexe |
R2n,l(r) | 4pr2Y2(r) | ||
n |
l |
m |
||||||
1 |
0 |
0 |
|
4e-2r | ||||
2 |
0 |
0 |
|
|||||
2 |
1 |
0 |
|
|||||
2 |
1 |
(±1) |
|
e±if | ||||
3 |
0 |
0 |
|
|||||
3 |
1 |
0 |
|
|||||
3 |
1 |
(±1) |
|
e±if | ||||
3 |
2 |
0 |
|
|||||
3 |
2 |
(±1) |
|
e±if | ||||
3 |
2 |
(±2) |
|
e±2if | ||||
4 |
0 |
0 |
|
|||||
4 |
1 |
0 |
|
|||||
4 |
1 |
(±1) |
|
e±if | ||||
4 |
2 |
0 |
|
|||||
4 |
2 |
(±1) |
|
e±if | ||||
4 |
2 |
(±2) |
|
e±2if | ||||
4 |
3 | 0 | 4fz3 |
|||||
Copyright Csonka Gábor István, BME