A Hartree-Fock-Rothaan-egyenletek zárthéjú molekulák esetében
A bevezetőben célszerű egy egységes jelölésrendszert megadni:
| Szimbólum | Jelentés |
| H | Egyelektron mátrix |
| F | Kételektron vagy Fock-mátrix |
| S | Átfedési mátrix |
| P | Suruség mátrix |
| A,B | Atom indexek |
| Z | Atommag vagy atomtörzs töltése |
| c | Atompálya |
| n, m, k, l | Atompálya indexek |
| z | Atompálya exponens |
| s, px, py, pz | s és p atompályák |
| j | Molekulapálya |
| i, j, k, l | Molekulapálya indexek |
| ei | Sajátértékek |
| a | Alfa spin |
| b | Béta spin |
| Dirac-féle integrál jelölés | |
| (ij,kl) | Kételektron-integrál |
| (i,j) | Átfedési integrál |
A hullámfüggvény
A 2n elektront tartalmazó zárthéjú rendszerek közelítő hullámfüggvényét a kétszeresen betöltött i pályákból felépített
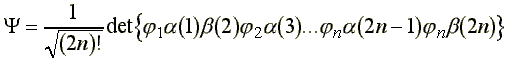
Slater determináns alakjában írhatjuk fel. A determináns kifejtési szabályát felhasználva :
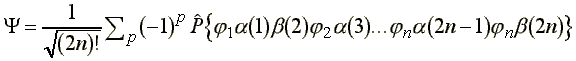
ahol P az 1, 2, 3, ..., 2n elektron permutációját eloállító operátor és (-1)p = +1, vagy -1 attól függően, hogy a p-edik permutáció páros vagy páratlan.
A![]() operátor az elektronok
koordinátáit permutálja, miközben a molekulapályák
sorrendje változatlan: ez összesen (2n)! permutáció.
Például, ha p az 1 2 3 4 számok 2 1 4 3 páros
permutációját írja elő, akkor:
operátor az elektronok
koordinátáit permutálja, miközben a molekulapályák
sorrendje változatlan: ez összesen (2n)! permutáció.
Például, ha p az 1 2 3 4 számok 2 1 4 3 páros
permutációját írja elő, akkor:
![]()
A fi molekulapályák ortonormáltan vehetők fel, azaz:
![]()
Ezek alapján![]() , vagyis
a hullámfüggvény normált (a bizonyítást
az olvasóra bízzuk). A molekula energiájának
várható értéke:
, vagyis
a hullámfüggvény normált (a bizonyítást
az olvasóra bízzuk). A molekula energiájának
várható értéke:![]()
ahol Y az elobb leírt determináns alakú függvény. A Hamilton operátort három részre bonthatjuk fel: H = HM + H1 + H2, ahol
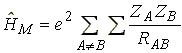 (1)
(1)
az atommagok közötti taszítás energiája (elektronkoordinátától független), N az atomok száma, ZA és ZB a magok töltése, RAB a magok távolsága,
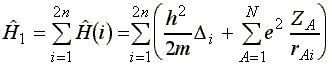 (2)
(2)
az elektron mozgását a csupasz atommagok elektrosztatikus terében írja le (egyetlen elektron koordinátájától függ), és ezt összegezni kell az összes 2n elektronra,
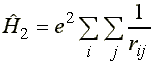 (3)
(3)
az elektronok taszítását leíró operátor, két elektron koordinátájától függ.
Az energia a következo alakbanban írható fel
![]() (4)
(4)
Az energia három részbol tevodik össze. Vizsgáljuk meg az egyes energia tagokat külön-külön.
1. A magok taszítási energiája:
![]() (5)
(5)
A magok közti taszítás kiszámításához
nincs szükségünk az elektronokra vonatkozó Y ismeretére,
mivel![]() nem függ az elektronkoordinátáktól.
Ez egy hasznos közelítés (Born-Oppenheimer). A molekula elektronenergiáját tehát
nem függ az elektronkoordinátáktól.
Ez egy hasznos közelítés (Born-Oppenheimer). A molekula elektronenergiáját tehát![]() és
és![]() határozza
meg.
határozza
meg.
2. Az egyelektronos rész energiája:
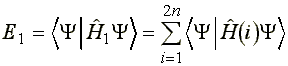 (6)
(6)
Mivel a molekulában található valamennyi elektron
esetében![]() azonos, elegendő
azonos, elegendő![]() figyelembevétele.
Így
figyelembevétele.
Így
![]() (7)
(7)
Y helyére Slater determinánst helyettesítve:
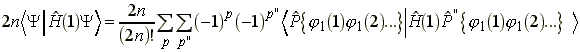
Az összes olyan lehetoség, amelyben![]() ,
a pályák és a spinfüggvények ortogonalitása
miatt az integráláskor nullát ad. Így a kettos
szummában csak azok a kifejezések különböznek
nullától, amelyekben
,
a pályák és a spinfüggvények ortogonalitása
miatt az integráláskor nullát ad. Így a kettos
szummában csak azok a kifejezések különböznek
nullától, amelyekben![]()
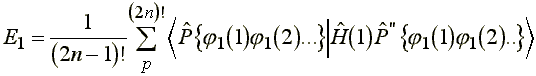 (8)
(8)
Mivel![]() csak az (1)-es elektront
tartalmazó molekulapályára hat, a többi 2, 3,
..., 2n elektron szerinti integrálás csupán egységnyi
szorzófaktort jelent. Ezért a kifejezés egyelektronos
integrálok összege, ahol valamennyi tagban az (1) elektron
tér és spin koordinátája szerint kell integrálni.
Mivel
csak az (1)-es elektront
tartalmazó molekulapályára hat, a többi 2, 3,
..., 2n elektron szerinti integrálás csupán egységnyi
szorzófaktort jelent. Ezért a kifejezés egyelektronos
integrálok összege, ahol valamennyi tagban az (1) elektron
tér és spin koordinátája szerint kell integrálni.
Mivel![]() független a spintol,
a spin szerinti integrálás újabb 1-es szorzófaktort
jelent.
független a spintol,
a spin szerinti integrálás újabb 1-es szorzófaktort
jelent.
Fusson végig i 1-tol n-ig valamennyi molekulapályán. Minden MO kétszer szerepel, egyszer a és egyszer b spinnel. Helyezzük az egyes elektront az i-edik MO-ra: fi(1)-re. Ekkor a többi 2n-1 elektront (2n-1)!-féleképpen tudjuk elhelyezni a többi szabadon maradó molekulapályán, Így:
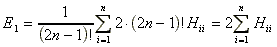 , ahol
, ahol
![]() (9)
(9)
A 2-es szorzófaktor megfelel annak, hogy minden i pályán két elektron található. Hii kiszámításához tehát csupán egyetlen elektron három térkoordinátája szerint kell integrálni, szemben az eredetileg 4×2n változós integrálással.
3. A kételektronos rész energiája
hasonló módon határozható meg. 2n elektronból![]() -féleképpen
választhatunk ki kettot. Ha két kiválasztott
elektron esetén meghatározzuk az összes lehetséges
kölcsönhatást, ezt egyszeruen be kell szoroznunk
-féleképpen
választhatunk ki kettot. Ha két kiválasztott
elektron esetén meghatározzuk az összes lehetséges
kölcsönhatást, ezt egyszeruen be kell szoroznunk![]() -vel,
és ezzel megkaptuk az összes elektronra érvényes
elektrontaszítási energiát. Válasszuk ki az
(1) és (2)-es elektront:
-vel,
és ezzel megkaptuk az összes elektronra érvényes
elektrontaszítási energiát. Válasszuk ki az
(1) és (2)-es elektront:
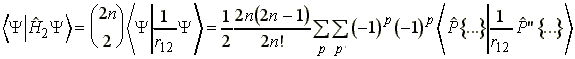 (10)
(10)
Az ortogonalitás miatt csak azok a kifejezések nem nullák,
ahol![]() vagy
vagy![]() csak
az 1 és 2 elektron felcserélésében különbözik
csak
az 1 és 2 elektron felcserélésében különbözik![]() -tol.
-tol.
a)![]()
Ekkor a két elektron két pályát
lefoglal, a többi elektron pedig (2n-2)!-féleképpen
helyezkedhet el. Ha az 1 és 2 elektron különbözo
fi és fj
térbeli pályán helyezkedik el![]() ,
akkor mindketto lehet a és b
spinu. Ez összesen négy lehetoség:
,
akkor mindketto lehet a és b
spinu. Ez összesen négy lehetoség:
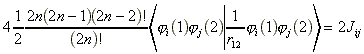 (11)
(11)
ahol Jij egy hatváltozós integrál.
Ha i=j,. akkor csak két lehetoség van, mivel a két
elektronnak ellentétes spinnel kell elhelyezkedni, az elektrontaszítási
járulék 2×1/2 Jii. A teljes elektrontaszítás:![]()
b) P csupán az 1 és 2 elektron koordinátáinak felcserélésében különbözik P"-től. Ha az 1 és 2 elektront a i és j molekulapályákhoz rendeljük, akkor négy lehetoség van:
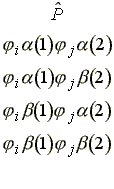
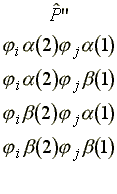
Vizsgáljuk meg az elso sort.
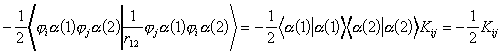 (12)
(12)
Látható, hogy mivel az operátor nem hat a spinekre,
azok külön integrálhatók az 1-es, ill. 2-es elektron
szerint, ami egy egyszeru szorzófaktort jelent, amellyel a
térbeli koordinátákat tartalmazó integrált,
(Kij)-t be kell szorozni. Itt![]() .
A második sor alapján:
.
A második sor alapján:
![]() mivel
mivel
![]() .
.
A harmadik sor kifejtése nullát ad, míg a negyedik
nem, ez -1/2 Kij, mivel![]() .
A negatív elojel onnan származik, hogy P és
P" éppen egy cserében különbözik, tehát
valamelyik szükségszeruen páratlan, míg
a másik páros, így
.
A negatív elojel onnan származik, hogy P és
P" éppen egy cserében különbözik, tehát
valamelyik szükségszeruen páratlan, míg
a másik páros, így![]() .
.
Ha a két elektront azonos pályához rendeljük (i = j), akkor spinjük biztosan különbözik, az integrál értéke nulla lesz.
Az elektronenergia valamennyi kölcsönhatást figyelembe véve:
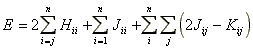 (13)
(13)
ahol az i index végigfut az összes fi kétszeresen betöltött molekulapályán. Ugyanez az egyenlet az összes eddigi megfontolás alapján a következo formában rendezheto:
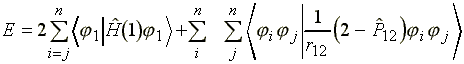 (14)
(14)
ahol![]() az 1 és 2 elektron
felcserélését végzo operátor.
Látható, hogy nem szükséges kikötni, hogy
az 1 és 2 elektron
felcserélését végzo operátor.
Látható, hogy nem szükséges kikötni, hogy
![]() ,
mivel ha i=j akkor 2Jii - Jii = Jii, ami helyes. Felhasználva hogy
Kii = Jii, az elektronenergia:
,
mivel ha i=j akkor 2Jii - Jii = Jii, ami helyes. Felhasználva hogy
Kii = Jii, az elektronenergia:
![]() (15)
(15)
A Hartree-Fock egyenletek molekulapályák esetében
A variációs elv alapján egy közelítés annál pontosabb, minél alacsonyabb a rendszer energiája. A legjobb determináns hullámfüggvényt úgy nyerjük, hogy az egyelektronos j1, j2, ..., jn függvényeket addig variáljuk, amíg az energia minimális lesz. Ezeket a pályákat nevezik "self-consistent" (önmagával összhangban lévo) Hartree-Fock (SCF HF) molekulapályáknak.
A variációt a feltételes szélsoérték
számításnál szokásos Lagrange-multiplikátor
módszerrel végezzük. Jelen esetben a feltételeket
a![]() ortogonalitási feltételek
szolgáltatják. E feltételeket egy határozatlan
szorzóval (multiplikátor) megszorozva és az eredeti
egyenlethez hozzáadva keressük az egyenlet szélsoértékét.
ortogonalitási feltételek
szolgáltatják. E feltételeket egy határozatlan
szorzóval (multiplikátor) megszorozva és az eredeti
egyenlethez hozzáadva keressük az egyenlet szélsoértékét.
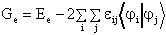 (16)
(16)
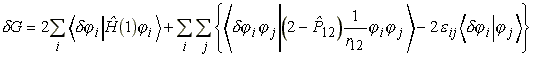 (17)
(17)
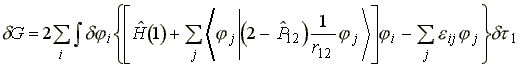 (18)
(18)
A kifejezés akkor nulla, ha a zárójelben levo mennyiség nulla:
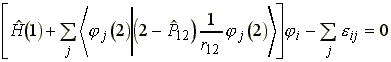 (19)
(19)
Vizsgáljuk meg a j-szerinti szummában szereplő integrálokat:
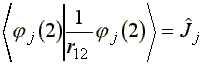 (20)
(20)
vagyis a Coulomb operátor kiszámítható és egy konstans szorzót jelent.
A![]() kicserélodési
operátor nem írható fel ilyen egyszeruen, hatását
a következo egyenlettel lehet leírni:
kicserélodési
operátor nem írható fel ilyen egyszeruen, hatását
a következo egyenlettel lehet leírni:
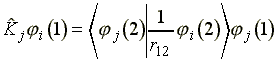 (21)
(21)
Ezekkel a jelölésekkel:
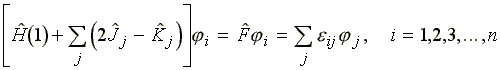 (22)
(22)
Az![]() operátor a Fock-féle
operátor. A variációszámítás
alapján megkapjuk ugyanennek az egyenletnek a komplex konjugáltját
is. Kimutatható, hogy eij Lagrange-multiplikátorokból
képzett mátrix önadjungált.
operátor a Fock-féle
operátor. A variációszámítás
alapján megkapjuk ugyanennek az egyenletnek a komplex konjugáltját
is. Kimutatható, hogy eij Lagrange-multiplikátorokból
képzett mátrix önadjungált.
Felhívjuk a figyelmet arra, hogy a fenti egyenlet nem sajátérték egyenlet, mivel az egyenlet jobb oldalán egy összeg szerepel. Ha ennek az összegnek csupán egy tagja különbözne zérustól, az egyenlet sajátértékegyenlet alakú lenne. Ez azt jelentené, hogy az e mátrix diagonális. Mivel az e mátrix szimmetrikus, unitér transzformációval diagonálissá alakítható.
![]() (23)
(23)
ahol T a transzformációs mátrix, e
a konstansok mátrixa, ediag
a diagonális mátrix,
![]()
ahol
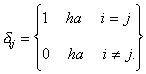 (24)
(24)
Diagonalizálás után a differenciálegyenlet rendszer a sajátérték egyenlethez hasonló formájú lesz
![]() (25)
(25)
Az összes i pálya ugyanazon önadjungált ![]() operátor
sajátfüggvénye, az
operátor
sajátfüggvénye, az ![]() operátor
tartalmazza azonban a
operátor
tartalmazza azonban a![]() és
és![]() operátorokon
keresztül magukat a pályákat is. Ezért a HF módszer
iteratív. A kiinduláskor fel kell tételezni
operátorokon
keresztül magukat a pályákat is. Ezért a HF módszer
iteratív. A kiinduláskor fel kell tételezni![]() pályákat,
majd ezek alapján ki kell számítani a
pályákat,
majd ezek alapján ki kell számítani a![]() és
és![]() operátorokat,
majd a Fock operátort. Az
operátorokat,
majd a Fock operátort. Az![]() operátor
sajátfüggvényei:
operátor
sajátfüggvényei:![]() segítségével
újabb
segítségével
újabb![]() operátort
állíthatunk össze, amely megint újabb sajátfüggvényeket
ad. Az iteráció akkor ér véget, amikor a sajátfüggvények
egy adott értéknél kisebb mértékben
változnak. Ekkor a betöltött pályák megfelelnek
a belolük szerkesztett Fock operátornak.
operátort
állíthatunk össze, amely megint újabb sajátfüggvényeket
ad. Az iteráció akkor ér véget, amikor a sajátfüggvények
egy adott értéknél kisebb mértékben
változnak. Ekkor a betöltött pályák megfelelnek
a belolük szerkesztett Fock operátornak.
A betöltött pályák felett léteznek magasabb ei sajátértékeknek megfelelo molekulapályák. Ezeket a betöltetlen pályákat virtuális pályáknak is hívják.
A Fock operátor sajátértékei:
![]() i = 1, n
(26)
i = 1, n
(26)
Minden ei energiát egy fi molekulapályához lehet rendelni, ezért ezeket pályaenergiának nevezik. A diagonális ei mátrixnak megfelelo molekulapályák delokalizáltak, azaz valamennyi atomot érintenek.
A HF LCAO-MO módszer zárthéjú molekulákban
Az elozo részben leírtuk, hogyan lehet az optimális molekulapályákat megkeresni egy nemlineáris, csatolt differenciálegyenlet-rendszer segítségével. Molekulák esetében az egyenlet ilyen formában történo megoldása gyakorlatilag lehetetlen.
Lényegesen kisebb számítási munkát jelent az az eljárás, amelyben a pályákat ismert függvények lineáris kombinációjával közelítjük. A legelterjedtebb módszer atompályák lineáris kombinációjából állítja össze a molekulapályát. Elonye a más típusú függvényeket használó módszerekkel szemben az, hogy az eredmények könnyen interpretálhatók, ugyanis a molekulák tulajdonságait gyakran az oket felépíto atomok viselkedésén keresztül érthetjük, ill. magyarázhatjuk meg. Ennek matematikai szempontból semmi jelentosége nincs.
Mivel ![]() , a molekulapályák
ortonormalitása az LCAO közelítésben a következoképpen
írható fel:
, a molekulapályák
ortonormalitása az LCAO közelítésben a következoképpen
írható fel:
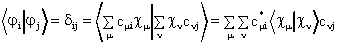 (27)
(27)
Az .![]() integrál, az
atompályák között értelmezett átfedési
integrál.
integrál, az
atompályák között értelmezett átfedési
integrál.
Vezessük be a következo mátrix jelöléseket: j = cC, illetve j+ = C+c+
A két egyenlet ugyanazt jelenti, csak egymás adjungáltjai, illetve valós értékek esetén egymás transzponáltjai:
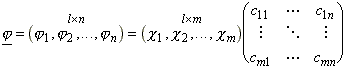 (28)
(28)
A transzponált egyenlet:
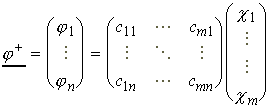 (29)
(29)
Ezeket a i molekulapályákat használjuk a determináns hullámfüggvényen belül. Az energia a korábbi levezetés értelmében:
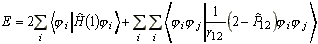 (30)
(30)
Elterjedten használják a következő, lerövidített, ún. töltéssűrűségi jelölést.
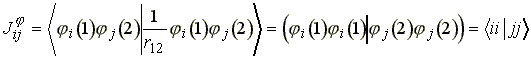 (31)
(31)
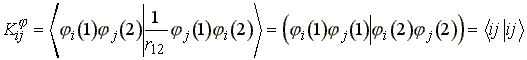 (32)
(32)
Az energia kifejezhető a következő egyenlettel ((15) egyenlet):
![]() (33)
(33)
ahol a felső index arra utal, hogy MO bázison fejtettük
ki az egyes operátorokat, a
![]() és
és
![]() a
Coulomb és cserélődési integrálokat
jelöli.
a
Coulomb és cserélődési integrálokat
jelöli.
A J és K integrált pszeudo egyelektronos integrálként
írhatjuk fel, ha definiáljuk
![]() pszeudo
egyelektronos önadjungált operátorokat.
pszeudo
egyelektronos önadjungált operátorokat.
![]() (34)
(34)
![]() (35)
(35)
Ekkor az energia:
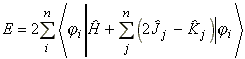 (36)
(36)
Variációszámítás segítségével a következő egyenlethez jutunk:
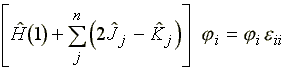 (37)
(37)
Az egyenlet jobb oldalán a zárójelben levő
operátorokat együttesen Fock operátornak (![]() )
nevezik.
)
nevezik.![]() (38)
(38)
ahol eii az i-edik MO energiája. A
Fock operátort az MO bázison reprezentáló mátrix
egy eleme:![]() (39)
(39)
A Fock operátor egyenletet mátrix egyenletté alakítva:
![]() ,
azaz
F= S e
(40)
,
azaz
F= S e
(40)
Mivel
![]() azaz egységmátrix,
a diagonális Fock-mátrix egyenlő az MO energia mátrix-szal:
azaz egységmátrix,
a diagonális Fock-mátrix egyenlő az MO energia mátrix-szal:
F = e.
(41)
A molekulapályákat az atompályákból
fogjuk felépíteni. A Fock operátor mátrixa
az atompályák bázisán:
F , melynek egy eleme:![]()
Szükség van még az S átfedési integrál
mátrixra, amelynek egy eleme: Smn=![]()
Az AO bázisról az MO bázisra hasonlósági
transzformáció segítségével térhetünk
át (mivel C uniter, C-1 = C+):
F=C+FC és S=C+SC
A Fock-féle mátrixegyenlet az AO bázison:
C+FC=C+SC
ahol F=H+2J-K
![]() (42)
(42)
![]() (43)
(43)
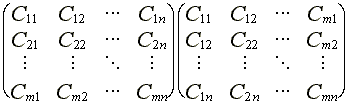
![]() (44)
(44)
ahol Pls
a P suruség mátrix
egy eleme: ![]() , azaz P =
C C+
, azaz P =
C C+
![]()
 (45)
(45)
Végül
![]() (46)
(46)
Röviden összefoglalva:
![]() (47)
(47)
Az energia AO integrálokkal kifejezve:
![]() (48)
(48)
Az egyenletet tovább egyszerusíthetjük
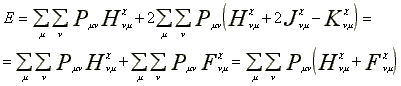 (49)
(49)
Az n belső index szerinti összegezés egy kijelölt mátrix szorzás:
![]() (50)
(50)
melynek eredménye egy szorzatmátrix diagonális
eleme. A diagonális elemek összege megadja az energiát: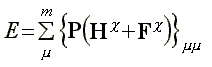 (51)
(51)
Vizsgáljuk meg milyen összefüggés van az összes elektronenergia és a pályaenergiák között. Korábban már bebizonyítottuk, hogy a Fock operátort reprezentáló mátrix az MO bázison egyszeruen az MO energiamátrix.
Az AO bázisról hasonlósági transzformációval térhetünk át az MO bázisra:
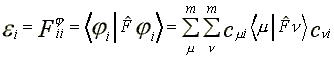 (51)
(51)
Ha az MO energiákat az összes betöltött molekulapályára összegezzük:
![]() (52)
(52)
Fejezzük ki![]()
![]()
Ha ezt behelyettesítjük, a következo eredményt kapjuk:
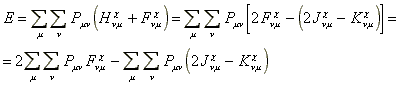 (53)
(53)
behelyettesítve a![]() kifejezést:
kifejezést:
![]() (54)
(54)
Az egyenlet alapján megállapítható, hogy az összes elektronenergia a betöltött MO energiák összegének kétszerese mínusz az elektrontaszítási járulék.
A számítások elvégzéséhez ismernünk kell az F mátrixot, amely P-tol függ. A P mátrixot viszont csak a C mátrix ismeretében tudjuk megszerkeszteni, de éppen ezt a mátrixot akarjuk kiszámítani. Ezért a sajátérték egyenlet csak iteratív módon oldható meg, azaz a korábban említett Self Consistent Field (SCF) módszerrel.
A megoldás során figyelembe kell vennünk, hogy az
atompályák nem ortogonálisak, ezért elso
lépésként a nem ortogonális atompályákat![]() ortogonálissá
ortogonálissá![]() ,
az atompályák bázisán képzett F mátrixot
pedig az ortogonális bázison képzett F mátrixszá
kell alakítanunk. Ezután diagonális alakra hozzuk
az utóbbi F mátrixot. A két traszformáció
megadja a koefficiens mátrixot.
,
az atompályák bázisán képzett F mátrixot
pedig az ortogonális bázison képzett F mátrixszá
kell alakítanunk. Ezután diagonális alakra hozzuk
az utóbbi F mátrixot. A két traszformáció
megadja a koefficiens mátrixot.
Mivel az ortogonalizáció egy speciális transzformáció, a C mátrixot célszeru két mátrixra bontani:
![]() , részletesen:
, részletesen:
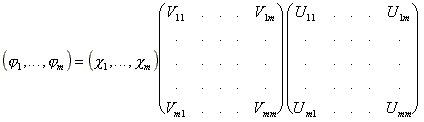 (55)
(55)
Oszlopmátrix jelöléssel:![]() (56)
(56)
Behelyettesítve a Hartree-Fock egyenletbe:
![]() (57)
(57)
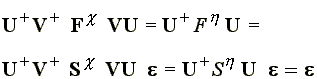 (58)
(58)
diagonális mátrix, az F mátrixot U-val diagonalizáljuk. Löwdin megmutatta, hogy a V ortogonalizáló mátrix S-1/2 mátrixnak veheto. Ezt a módszert hívják szimmetrikus vagy Löwdin ortogonalizációnak.
Az S-1/2 mátrix megkeresése a diagonális mátrixok speciális tulajdonságai alapján lehetséges, ugyanis ha a diagonális elemeken valamilyen muveletet végrehajtunk, ez megfeleltetheto az egész mátrixon elvégzett muveletnek. Ezért az S szimmetrikus valós mátrixot unitér transzformációval diagonalizáljuk: (D), majd a diagonális elemeket a -1/2-ik hatványra emeljük, végül ezt a diagonális mátrixot visszatranszformáljuk nem diagonális alakba. Legyen T ortogonális mátrix az, amely S-et diagonalizálja (az unitér valós mátrixot ortogonálisnak nevezzük):
T+ S T = D (59)
A visszatranszformálás a következoképpen történik:
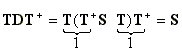 (60)
(60)
A D-1/2 mátrixot visszatranszformálva:
S-1/2 = T D-1/2 T+ (61)
Ellenorizzük a V+ S V = 1 egyenloség fennállását, ha V = S-1/2:
V+ = (T D-1/2 T+)+ = (T+)+ (D-1/2)+ T+ = T D-1/2 T+ (62)
a (D-1/2)+ = D-1/2 , mivel diagonális, és
V+ S V = (T D-1/2 T+)+ S (T D-1/2 T+) = T D-1/2 D D-1/2 T+=
= T D D-1 T+ = T T+ = 1 (63)
A bizonyítás során felhasználtuk, hogy a diagonális mátrixok felcserélhetok a mátrix szorzásra nézve és hogy D-1/2 × D-1/2 = D-1
Az SCF ciklussal kapcsolatos technikai részletek
A bázisfüggvények számának (m) függvényében a kiszámítandó egyelektron-integrálok száma: K1 = m(m+1)/2 és a kételektron-integrálok száma: K2 = K1(K1 + 1) gyorsan no:
| m = | 10 | 50 | 100 |
| K1 = | 55 | 1275 | 5500 |
| K2 = | 4540 | 814725 | 12751250 |
Ez alapján érthető, hogy a kvantumkémiai számításoknál miért a bázisfüggvények integráljainak kiszámítása, tárolása és feldolgozása a legnagyobb feladat. Ezek az integrálok egy bizonyos távolság felett elhanyagolhatoan kicsivé válnak és ez lehetové teszi nagyobb molekulák viszonylag gyors kiszámítását (a számítási igény növekedése joval alacsonyabb a negyedik hatványnál, ügyes szervezéssel a harmadik hatvány alá lehet szorítani a számításigényt). A közelíto módszerek általában a kételektronos-integrálok jelentos részét elhanyagolva gyorsítják meg a számítást.
A HF-Roothan SCF ciklusok szervezését a következo oldalon található folyamatábra szemlélteti. Néhány megjegyzés a folyamatábrával kapcsolatban:
A folyamatábra szerint a konvergenciát az energia konvergenciáján keresztül követjük. A teljes energia (E) az iterációs ciklusok során monoton csökken. A konvergenciát két egymást követo iterációban kiszámított energiák abszolutértékének különbségén keresztül lehet követni: (DE = |En-1 - En|). Ha ez a különbség egy elore megadott, kicsi eps < 10-6 küszöbnél kisebb, az iterációt befejezzük és a végeredményt kiiratjuk. Gyakran használják ezen kívül a suruség-függvény mátrixának (P) konvergenciáját. Ez utóbbi felel meg az SCF eredeti elgondolásának, hiszen közvetlenebbül, a pályafüggvények eltérésén keresztül követi a konvergenciát. A gyakorlatban az energia a függvény javulásával párhuzamosan mélyül, így ez a konvergencia kritérium is sikerrel alkalmazható.
Végül vizsgáljuk meg, milyen következménnyel jár, ha a legegyszerubb (C = 0) koefficiens mátrixszal indítjuk az iterációt. Ebben az esetben a suruségmátrix szintén nulla mátrix (P = 0), és az összes olyan kifejezés, amelyben szerepel (J, K és E) szintén nulla lesz. Az F mátrix azonban nem lesz nulla, mert az F = H + 2J - K egyenletben csak az utolsó két tag nulla. Így az F = H közelítést használjuk.
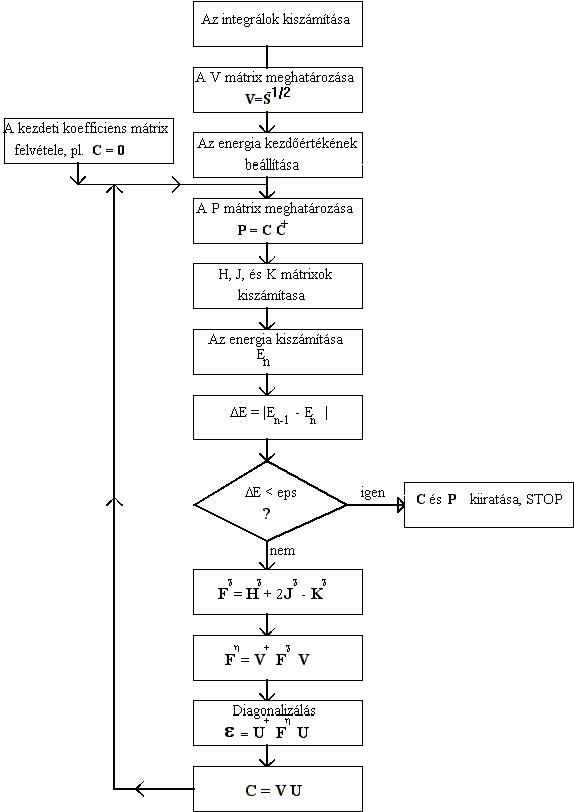
A HF-Roothan SCF ciklusok szervezése
Populációs analízis
A delokalizált molekulapályák jól leírják a molekula elektronszerkezetét, de nem adnak szemléletes képet azokról a változásokról, amelyek a kémiai kötés kialakulásához vezetnek. Ahhoz, hogy a kémiában gyakran használatos töltés és kötésrend fogalmak egyáltalán megjelenjenek a kvantumkémiai leírásban, matematikai transzformációkra van szükség. Az alapveto és csaknem felodhatatlan probléma az, hogy a molekulán belül az atomok töltése és kötésrendje közvetlenül nem mérheto, így a számított értékeket nem lehet kísérletileg ellenorizni.
Több különbözo matematikai eljárás ismert töltések és kötésrendek kiszámítására, de ezek önkényes feltételezéseken alapulnak, és az eredmények nagyon erosen függenek az alkalmazott bázistól is. Ebbol következik, hogy csak azonos bázison számított populációs analízisek összehasonlításának van értelme. Az atompálya populációknak csak minimális bázison van értelme.
A molekulák elektrosztatikus potenciál térképe lehetové tesz egy fizikailag ellnorizheto töltés definíciót, ami az utóbbi idoben új lendületet adott a molekulában lévo atomok töltésével kapcsolatos kutatásoknak. A töltéseket úgy definiálják, hogy a leheto legjobban reprodukálják a kísérleti és/vagy elméleti elektrosztatikus potenciálokat.
A Mössbauer spekroszkópia segítségével a magokban észlelheto elektronsuruséget tudjuk mérni.
A Mulliken-féle populációs analízis
Az MO-k az AO-k lineáris kombinációi:![]()
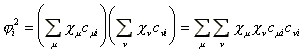
![]() -et az egész
térre integrálva, megkapjuk a pálya populációt,
Ni-t:
-et az egész
térre integrálva, megkapjuk a pálya populációt,
Ni-t:
![]()
ahol Smn az átfedési integrál. Az összes MO-ra összegezve kapjuk a következo egyenletet:
![]()
ahol N a molekulában levo összes elektron száma.
Az egyenletbol látható, hogy a betöltési számot (Ni) figyelembe kell venni a suruségmátrix kiszámításánál. Zárthéjú molekulák esetén minden betöltött pályán két elektron van (Ni = 2), ami kiemelheto:
![]()
Az átfedési populációs mátrix a következoképpen definiálható:
![]()
Mivel P és S szimmetrikus, a Pop mátrix is szimmetrikus. A diagonális elemek az atompálya elektron populációját (Pm), betöltését reprezentálják, a nem diagonális elemek megfeleltethetok az átfedési atompálya-populációnak. Vizsgáljuk meg hogyan lehet a teljes töltést a bázisfüggvények között szétosztani. Egy lehetséges mód, hogy a Popmn -t egyenlo arányban osztjuk fel a n és m indekszu bázisfüggvények között és hozzáadjuk Pm-höz.. Ekkor a m-edik pálya ún. teljes populációja:
![]() , ahol
, ahol![]() .
.
Ez a felosztási megoldás csak egy a lehetséges sokféle felosztási mód közül.
Az A atomhoz tartozó bázissfüggvények populációit összeadva megkapjuk az atom teljes atomi populációját:
![]()
Az A atom nettó töltése QA= ZA - qA, ahol ZA A atom magjának töltése.
Ha az A és B atomok között eloforduló összes Popmn elemet összegezzük, megkapjuk a két atom közötti teljes átfedési populációt, amit a kötésrenddel lehet összefüggésbe hozni:
![]()
Az atomok közötti átfedési populáció az atomok közötti kötésrol nyújt kvantitatív információt.