y = r sin(q) sin(f) és
z = r cos(q).
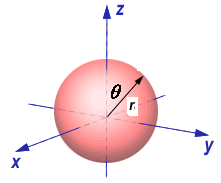
A hidrogén atompályáinak normált, analitikus alakja az atommagtól mért távolság (r, atomi egység) és a térszögek (
q, f) függvényében.A tömörség és a jobb áttekinthetőség kedvéért a szögeket a derékszögű koordináta tengelyre eső vetületükkel jelöljük, így:
 |
x = r sin(q) cos(f), y = r sin(q) sin(f) és z = r cos(q). |
Ezt behelyettesítve megkaphatjuk a szögektől függő kifejezéseket is.
A Y(r,q,f) függvényt célszerű két egyszerűbb függvény szorzataként felírni: Y(r,q,f) = Rn,l(r).Yl,m(q,f) ezzel a háromváltozós
Y függvényt felbontottuk egy egyváltozós és egy kétváltozós függvény szorzatára.Megjegyzendő, hogy tetszőleges Z rendszámú atom analitikus függvénye a következőképp származtatható az alábbi függvényekből: a radiális részben, Rn,l(r), az r-t helyettesíteni kell r.Z-vel és a preexponenciális tényezőt szorozni kell Z(3/2+l)-el, ha atomi egységben számolunk. Más távolság egységre az a0 = 52.918 pm összefüggés segítségével számíthatók át az eredmények.
Ha az atompálya jelére kattintunk megjelenik az atompálya 3 dimenziós, interaktiv képe (kellék: BS Contact ingyenesen letölthető VRML megjelenítő). Az azonos hullámfügvény abszolút értékekhez tartozó pontok láthatók egy felületként (angolul iso surface). Mivel a hullámfüggvény előjelet vált ezért eltérő színnel jelöljük a pozitív és negatív értékekhez tartozó felületeket (kék és sárga). Az itt ábrázolt pályák valós függvények, viszont azt tudni kell, hogy a Schrödinger egyenlet megoldásakor a nem nulla mágneses (m) kvantumszámú pályák komplexek (pl. a három p pálya közül kettő komplex). Ezt a két komplex pályát lineáris kombinációval a valós térbe lehet vetíteni és így megkapható belőlük a px és a py valós pálya. Viszont ezekhez a vetített pályákhoz már nem rendelhető mágneses kvantumszám. A komplex részt a p és d pályák esetében külön jelöljük.
|
Kvantumszámok |
Jelölés |
Radiális Rn,l (r) |
Szögfüggő valós Yl,m(q,f) |
Komplex tag |
R2n,l(r) | 4pr2Y2(r) | ||
n |
l |
m |
||||||
1 |
0 |
0 |
|
4e-2r | ||||
2 |
0 |
0 |
|
|||||
2 |
1 |
0 |
|
|||||
2 |
1 |
(±1) |
|
e±if | ||||
3 |
0 |
0 |
|
|||||
3 |
1 |
0 |
|
|||||
3 |
1 |
(±1) |
|
e±if | ||||
3 |
2 |
0 |
|
|||||
3 |
2 |
(±1) |
|
e±if | ||||
3 |
2 |
(±2) |
|
e±2if | ||||
4 |
0 |
0 |
|
|||||
4 |
1 |
0 |
|
|||||
4 |
1 |
(±1) |
|
e±if | ||||
4 |
2 |
0 |
|
|||||
4 |
2 |
(±1) |
|
e±if | ||||
4 |
2 |
(±2) |
|
e±2if | ||||
4 |
3 | 0 | 4fz3 |
|||||
A Y(r,q,f) függvény négyzete megadja az elektronsűrűséget. A Y2(r,q,f) -et 4pr2-tel beszorozva megkapjuk a radiális elektronsűrűséget:
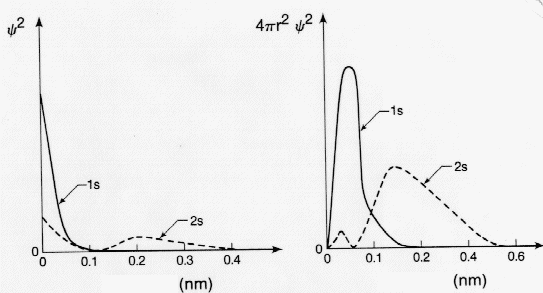
Az 1s és a 2s pályák négyzete és radiális elektronsűrűségük a távolság függvényében (nm).
Copyright Csonka Gábor István, BME