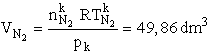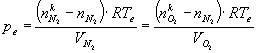1. Megoldás:
    A "normál körülmények" 0 oC-t és 101,325 kPa nyomást jelentenek. Az egyesített gáztörvényt alkalmazva:


    2. = 362,16 cm3

    Megjegyezzük, hogy természetesen ugyanehhez az eredményhez jutunk, ha mindkét nyomást a régebben használatos Hgmm-ben vagy atm-ban helyettesítjük be.

  2. Megoldás:

    = 607,95 kPa

    T1 = T2
  3. Megoldás:
    A palackban maradó gáz az eredeti gázmennyiségnek 75%-a, amely a palack térfogatának 75%-át foglalta el. Eszerint a gáz kezdeti állapotának állapothatározói:
    p1 = 16,2 MPa
    V1 = 0,75 V, ahol V = a palack térfogata
    T1 = 300 K
    Végállapotának állapothatározói:
    p2 = ?
    V2 = V
    T2 = 280 K
    Az egyesített gáztörvény szerint:



    p2 = 11,34 MPa
  4. Megoldás:
    Az általános gáztörvényt alkalmazva a kezdeti és a végállapotra:

    5.  







    = 23,9435 g

    Ha a térfogatot literben (dm3-ben), a nyomást pedig kPa-ban helyettesítjük be a Dm képletébe, akkor R értéke 8,314, minthogy a korábbiakban láttuk, hogy R = 8,314 N· m/K· mol, a Pa-ról a kPa-ra való áttérés 10-3-nal való szorzást, a m3-rol a dm3-re való áttérés pedig 103-nal való szorzást jelent, tehát R értéke nem változik. A korábban használatos nyomásegységben (atmoszférában) kifejezett nyomást behelyettesítve, az R = 0,082 l· atm/K· mol értékkel kell számolnunk.

  5. Megoldás:
    Az egyesített gáztörvény segítségével kiszámíthatjuk az új körülmények között a gáz térfogatát.


    6. D V = 950 l

    Tehát egy 950 l űrtartalmú tartállyal kell a palackot összekötni.

  6. Megoldás:

    , T2 =

    7. t = 163,58 oC

  7. Megoldás:
    a.) Avogadro törvényét alkalmazva:
    gramm-moltömegű (molnyi) gáz térfogata normál körülmények között 22,414 l. Tehát:

    28 g nitrogén 22,414 l térfogatú
    x g nitrogén 1 l térfogatú

    x = = 1,2492 g
    b.) Az általános gáztörvényt alkalmazva:





    = 1,2492 g
  8. Megoldás:
    Mindkét állapotra az általános gáztörvényt alkalmazva

    9. = 51,26 kPa

  9. Megoldás:
    Avogadro törvénye alapján gázok relatív sűrűsége (dr) moltömegük arányával kifejezhető:



    10. ; ;

    ; ; .


    Minthogy mólnyi gáz normál térfogata 22,414 liter, egyszerű aránypárral kiszámítjuk a fenti gázok normál litertömegét.

    = 1,25 g; = 1,52 g; = 1,96 g; = 3,17 g:
    = 2,85 g; = 1,34 g; = 2,05 g.

  10. Megoldás:
    Az általános gáztörvényt alkalmazva:




    11. M = 4,03, tehát He-ról van szó.

  11. Megoldás:
    Dalton törvénye értelmében a gázelegy össznyomása a komponensek parciális nyomásaiból additíve tevődik össze:

    12. A gázelegy valamennyi komponensére érvényes a

    pö · Vi = Vö · pi

    összefüggés, vagyis

    , ahol a térfogattört.

    Tehát = 0,34, = 0,66

    A térfogattört a térfogatszázalék század része, így a gázelegy összetétele a következő:

    34 (V/V)% NO és 66 (V/V)% NO2.

  12. Megoldás:
    Mivel a gázok esetében a térfogattört megegyezik a moltörttel, a parciális nyomást a következőképpen is kifejezhetjük:







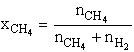
    13. kPa

  13. Megoldás:
    A nitrogén parciális nyomása
    kPa
    , cm3
  14. Megoldás:
    A példa megfogalmazásából kitűnik, hogy izobar körülményt tartunk fenn. Felírhatjuk a kezdeti és a végállapotban a komponensek parciális nyomásait kezdeti állapotban:


    15. végállapotban:


    A két gáz parciális nyomása úgy aránylik egymáshoz, mint molszámaik (ld. Dalton és Amagat szabály).

    Kezdeti állapotban: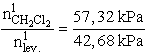

    Végállapotban: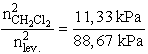


    A két egyenletet egymással elosztva megkapjuk, hogy az eredeti metilén-klorid hányad része marad a lehűtés után a gázelegyben.



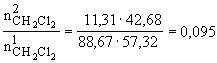
    = 0,095


    Tehát az elegyben 9,5% metilén-klorid marad vissza és 90,5% nyerhető vissza. A kérdés 10 m3 elegyből visszanyerhető anyag mennyiségére vonatkozott. Meg kell tehát határoznunk, hogy 10 m3 elegyben hány mol metilén-kloridunk van. Az egyetemes gáztörvény összefüggését alkalmazva kapjuk:

    = = 231,23 mol

    Ennek 90,5%-a visszanyerhető:
    = 209,26 mol, ill. a moltömeggel szorozva
    = 209,26· 85

    = 17787,1 g = 17,79 kg CH2Cl2 nyerhető vissza 10 m3 levegőből hűtéssel.

  15. Megoldás:
    a.) A tökéletes gáz közelítés alapján:

    16. Ilyen nagy nyomáson azonban a tökéletes gáz közelítés nem ad megfelelő eredményt. Valóban, a mérés alapján a nyomás 5,06 MPa. Ebben az esetben már nem tekinthetünk el a részecskék közötti kölcsönhatástól és a részecskék saját térfogatától sem.

    b.) Vizsgáljuk meg, milyen eredményt kapunk a van der Waals egyenlet alapján.

    , ahol

    a = 3,648· 105 l2 · Pa/mol2
    b = 0,0428 l/mol


    Látható, hogy a méréssel való egyezés lényegesen jobb.

  16. Megoldás:
    104,33 kPa
  17. Megoldás:
    33,2 l O2 , 44,83 l N2, 5,6 l l SO2, 7,47 l NO, 3,2 l CO, 5,6 l CO2, 224,14 l H2, 44,83 l Cl2
  18. Megoldás:
    1/5 részt kell kiengedni, 192,78 kPa
  19. Megoldás:
    2,837 MPa
  20. Megoldás:
    1/20  részt kell kiengedni, 192,78 kPa
  21. Megoldás:
    a gáz hőmérséklete háromyszorosára nő.
  22. Megoldás:
    1,963 g/l C3H8,0,714 g/l CH4,3,476 g/l AsH3,4,6397 g/l SiF4, 5,706 g/l HI
  23. Megoldás:
    20,17 ; 20,17 ; 20,18
  24. Megoldás:
    254,1 g/mol
  25. Megoldás:
    135 g/mol ; S2Cl2
  26. Megoldás:
    2,244 ; 2,700 g/l
  27. Megoldás:
    S6
  28. Megoldás:
    1,628 g/l
  29. Megoldás:
    6,02·1021
  30. Megoldás:
    21,28 kPa ;28,84 g/mol
  31. Megoldás:
    106,65 kPa ; pO2=26,66 kPa ; pCH4=79,99 kPa
  32. Megoldás:
    99,97 kPa
  33. Megoldás:
    83,2 kPa
  34. Megoldás:
    101,17 kPa
  35. Megoldás:
    10,21 MPa
  36. Megoldás:
    0,881 g/l
  37. Megoldás:
    133,6 g/mol
  38. Megoldás:
    pO2=47,00 kPa
  39. Megoldás:
    M=6,65 g/mol ; 66,7% H2, 33,3 tf% CH4 , 20% H2, 80% CH4 , Sr=0,229
  40. Megoldás:
    A Van der Waals egyenlet állandói a kritikus állapot jellemzőinek segítségével nyerhetők a következő összefüggés alapján:

    ahol pK és vk a a kritikus állapothoz tartozó nyomás, illetve térfogat
    pK = 4,56 MPa; Vk = 271,210-6 dm3; a = 1,006 Pa dm6, b = 9,0410-5 dm3
  41. Megoldás:
    1. A felmelegítés után a gáz összmolszáma a levegő és a kámfor moljainak összege.
      ,
      —
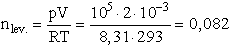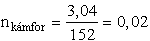
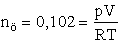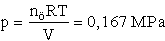
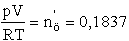    2. nkámfor = nö-nlev. = 0,1017

      mkámfor = 152·0,1017 = 15,46 g
  42. Megoldás:
    M=44,03 g/mol C2H4O
  43. Megoldás:
    pSO2=58,2 Pa ; mSO2=1,4778 g
  44. Megoldás:
    96,6%-a van cseppfolyós állapotban
  45. Megoldás:
    Nem távozik levegő
  46. Megoldás:
    15,27%-al csökken a lufi térfogata
  47. Megoldás:
    44 g
  48. Megoldás:
    900 kPa-ig használható
  49. Megoldás:
    8,328 MPa
  50. Megoldás:
    5,73 m3
  51. Megoldás:
    386,2 kPa
  52. Megoldás:
    16,4% O2, 61,6% N2, 22% H2
  53. Megoldás:
    Tekintve, hogy a tökéletes gáztörvény szempontjából mind a négy gáz azonos módon viselkedik - a gáztörvény független az anyagi minőségtől - csak az összmolszám érdekes. Ezért a reakcióegyenlet lényege


    54. 2 mol folyadékból (nitropentaeritritbol, vagy röviden nitropentából) 25 mol gáz lesz, azaz


    nf : ng = 2 : 25, 25 nf  = 2 ng

    Gáztörvénybe helyettesítve: , továbbá

    25 d = p =

    = 1731,6·106 Pa = 1732 Mpa

  54. Megoldás:
    86,87 g
  55. Megoldás:
    Kezdetben:

mol

mol


A hőmérséklet megváltozása miatt a nitrogéntartályban nő, az oxigéntartályban csökken a nyomás, így az új egyensúlyi állapot úgy jöhet létre, ha nitrogén áramlik át az oxigéntartályba, míg a nyomások újra egyenlők nem lesznek.




Az egyenletbe behelyettesítve és megoldva kapjuk:

pe = 100 kPa (V/V)% O2 = mol% O2 = 60%

  1. Megoldás:
    8,23 l
  2. Megoldás:
    1,069 g/l
  3. Megoldás:
    301 kPa, 234 kPa
  4. Megoldás:
  5. Megoldás:
    1:3
  6. Megoldás: