A víz és gőz között
egyensúlyt feltételezve, DG = 0, így
DH= TDS
ezért
![]()
A megfelelő
![]() értékek:
értékek:
CuO(sz) + H2(g) = Cu(sz) + H2O(f)
![]() : -129,7 0 0
-237,1 (kJ/mol)
: -129,7 0 0
-237,1 (kJ/mol)
ebből:
DG0 = (0 - 237,1) - (-129,7 + 0) = -107,4 kJ
A réz(II)-oxid redukciója H2 gázzal 25 oC-on tehát önként
végbemenő (spontán) folyamat.
- DG0 = -1370,8 kJ; jobbra
- DG0 = -32 kJ; jobbra
- DG0 = -130,2 kJ; jobbra
- DG0 = -238,2 kJ; jobbra
- DG0 = 345,7 kJ; balra
- DG0 = -83,9 kJ; jobbra
- DG0 = -871 kJ; jobbra
- DG0 = 238,2 kJ; balra
Először Kc-t fejezzük ki;
![]()
majd behelyettesítjük a megfelelő egyensúlyi koncentrációkat:
![]()
Kn értékének számításához először az egyensúlyban lévő molszámokat kell megtalálni.
| A + | 3 B | Ű | 2 C | |
| Kezdeti: | 2 | 4 | 0 | |
| Reagáló: | ? | ? | +2 | |
| A reakcióegyenletből megtudhatjuk a reagáló molszámokat. Két mol "C" anyag 1 mol "A" anyagból és 3 mol "B" anyagból keletkezik. Ennek megfelelően | ||||
| Reagál: | -1 | -3 | +2 | |
| Egyensúlyban: | ? | ? | 2 | |
| Nyilvánvaló, hogy az egyensúlyi "A" és "B" anyagok molszáma a kezdeti és az elfogyott molok közötti különbség. Így | ||||
| Egyensúlyban: | (2-1) | (4-3) | 2 | |
| azaz | 1 | 1 | 2 | |
lesznek a molszámok. Most már Kn számítható:
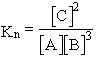
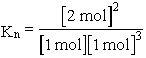
![]()
A reakcióegyenlet és a molok száma:
| CO(g) + | 2 H2(g) | Ű | CH3OH(g) | |
| Kezdeti : | 1 | 2 | 0 | |
| Reagált : | 0.3 | 2·0.3 | 0.3 | |
| Egyensúlyi: | 0.7 | 1.4 | 0.3 |
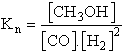
![]()
S ni = 0,7 + 1,4 + 0,3 = 2,4 mol
Dn = -2
Kp = 0,2186 mol-2.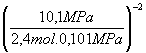
Kp = 1,26×10-4
pHCl = 42,34 kPa, pO2 = 10,58 kPa, pCl2 = 24,04 kPa, pH2O = 24,04 kPa
Kx = 0,992, Kp = 0,992, Kc = 70,99 dm3/mol , Kn = 0,222
Tételezzük fel, hogy a PCl5 koncentrációja x mollal csökkent a reakció során.
| PCl5(g) | Ű | PCl3(g) + | Cl2(g) | |
| K: | 0,12 | 0 | 0 | |
| R: | -x | +x | +x | |
| E:: | 0,12-x | x | x |
![]()
ebből x kifejezhető:
x2 + 0,8x - 0,096 = 0
![]()
Az egyenlet másik megoldása negatív koncentrációt adna, ami értelmetlen és nem
lehetséges. "x" értékéből mindegyik komponens koncentrációja
számítható.
- Először Kn-t számítsuk ki, majd azután Kp-t. Tételezzük
fel, hogy A2 kezdeti mennyisége n0.
K: n0 0 R: -n0 a 2 n0a E: n0(1-a) 2 n0a S ni = n0(1+a)
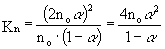
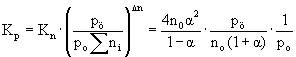
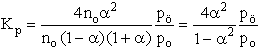
- Először számítsuk ki a parciális nyomásokat, azután Kp-t:
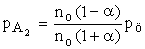
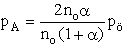
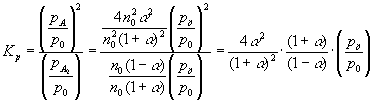
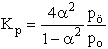
A tökéletes gáztörvények alapján az egyensúlyi összmolszám egyszerűen számítható:
Ebből az átlagos moltömeg:
Ismerjük az eredeti N2O4 molszámot
Vizsgáljuk meg az egyensúlyi molarányt:
| N2O4(g) | Ű | 2 NO2(g) | |
| K: | 0,02174 | 0 | |
| R: | -x | 2x | |
| E: | 0,02174-x | 2x |
Sni = 0,02174 - x + 2x = 0,03555
Az egyenletből x értéke kiszámítható, x = 0,01381,
2x = ![]() =
0,02762 mol
=
0,02762 mol
![]() = 0,02174 - x =
0,02174 - 0,01381 = 0,00793 mol
= 0,02174 - x =
0,02174 - 0,01381 = 0,00793 mol
Most már kiszámíthatjuk Kn-t:
![]()
Végül kiszámíthatjuk a disszociációfokot is. Ha 0,02174 molból 0,01382 mol
bomlik, akkor 1 molból a
![]()
A reakcióegyenlet és a megfelelő molok:
| A | Ű | kB | |
| K: | 1 | 0 | |
| R: | -a | k a | |
| E: | 1-a | k a |
Sni = 1-a + ka = 1 + (k-1)a
Az átlagos moltömeg:
![]()
M = 114,3 g/mol
Az egyensúlyi összmolszám (1 mol kiindulási anyagot feltételezve),
mint a kezdeti moltömeg és az egyensúlyi átlagmoltömeg hányadosa számítható ki:
![]() ebből
ebből
![]()
![]()
A reakcióegyenletből látható, hogy csak a CO2 van gázfázisban:
CaCO3(sz) Ű CaO(sz) + CO2(g)
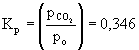 .
. Mivel
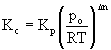
Kc = 7,02× 10-3
A sósav erős sav, ezért teljes mértékben disszociál és H3O+ ionokat képez. A következő reakcióegyenletet vizsgálva látható, hogy a H3O+ koncentráció a kiindulási savkoncentrációval egyenlő:
HCl + H2O Ű H3O+ + Cl-
így a teljes [H3O+] a sav és a víz disszociációjából származik:
[H3O+]t = [H3O+]sav + [H3O+]víz = 2×10-2 + [H3O+]víz = 2×10-2 mol/dm3
A vízből származó [H3O+]víz értéke semleges közegben 10-7 mol/dm3. Savas közegben ez az érték még kisebb, ezért elhanyagolható.
pH = -lg 2×10-2 = 1,699.
- Ha a fentiek során alkalmazott módszert mechanikusan ismételnénk, a következő
helytelen eredményt kapnánk:
[H3O+] = 10-8 M, tehát pH = 8,00
Természetesen ez lúgos közeget jelent, ami egy sav oldat esetében képtelenség. Ebben az esetben ugyanis az igen kis [H3O+]sav koncentráció miatt már nem lehet figyelmen kívül hagyni a [H3O+]víz értéket.
- Tételezzük fel egy pillanatra, hogy [H3O+]víz = 10-7
a savas oldatban, azaz ugyanannyi, mint a semleges kémhatású vízben. Ebben az esetben:
[H3O+]t = [H3O+]sav + [H3O+]víz = 10-8 + 10-7 = 1,1.10-7 M
pH = -log 1,1× 10-7 = 6,96
- A fenti feltételezés nem helyes, amikor ugyanis savat öntünk a vízbe, akkor az
eredeti [H3O+]víz értéke az egyensúlyi reakció
során megváltozik, így nem lehet állandó értékűnek tekinteni. Viszont kezdeti
koncentrációul választhatunk 10-7 M-t:
2 H2O = H3O+ + OH- K: 1,1×10-7 10-7 R: -x -x E: 1,1× 10-7 - x 10-7 - x Kv = (1,1× 10-7 - x)(10-7 - x) = 10-14 M2
ebből
x2 - 2,1× 10-7x + 10-15 = 0
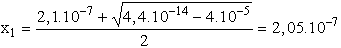
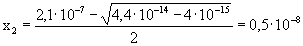
behelyettesítve [H3O+]t-be:
[H3O+]t,1 = 1,1× 10-7 - 2,05× 10-7 = negatív szám, nem értelmezhető.
[H3O+]t,2 = 1,1× 10-7 - 0,5.10-8 = 1,05× 10-7M
pH = 6,98 - Kevesebb számítás várható, ha kezdeti koncentrációként csak a savból származó
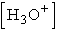 -t vesszük
figyelembe:
-t vesszük
figyelembe:
2 H2O Ű H3O+ + OH- K: 1·10-8 0 R: +y +y E: 10-8 +y +y Kv = (10-8 + y)y = 10-14 M2
Eredetileg disszociálatlan vizet tételeztünk fel. Ebből:
y2 + 10-8y - 10-14 = 0
kifejezve y-t:
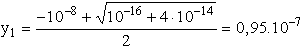
y2 = negatív szám, értelmetlen
[H3O+]t = 10-8 + 9,5× 10-8 = 10,5× 10-8 = 1,05× 10-7;
pH = 6,98
Ugyanazt a logikai sorrendet használhatjuk, amit már a gázegyensúlyoknál alkalmaztunk. Először kiszámítjuk a disszociációfok segítségével az egyensúlyi koncentrációkat, majd felírjuk az egyensúlyi állandót alkotó megfelelő kifejezést:
| CH3COOH | + H2O Ű | H3O+ + | CH3COO- | |
| K: | 2 | 0 | 0 | |
| R: | -2a | 2a | 2a | |
| E: | 2(1-a) | 2a | 2a |
![]()
- Ha a elég kis érték (kisebb, mint 0,05), akkor a nevezőben elhanyagolható:
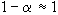 . Így Kc
= 2 a2, ebbol a = 2,98× 10-3
. Így Kc
= 2 a2, ebbol a = 2,98× 10-3
[H3O+] = 2× 2,98× 10-3, pH = 2,23
- Bár a értéke láthatóan kicsi, tehát feltételelezésünk (a « 0,05) helytálló
volt, mégis hasonlítsuk össze a pontos számítással (amely kissé körülményesebb).
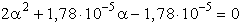
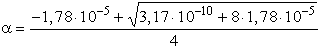
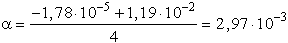
pH = 2,23
HNO2 Ű H+ + NO2- K: 1 0 0 R: -a a a E: 1-a a a 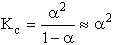 (feltételezve, hogy a « 0,05).
(feltételezve, hogy a « 0,05).a = 2·10-2, ami feltevésünket igazolta.
- Ismét tételezzük fel, hogy a értéke a tört nevezőjében elhanyagolható:

ebből a = 0,2, azaz feltevésünk helytelen volt.
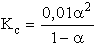 és
és 
A fenti példából levonható az az általános következtetés, hogy a disszociáció foka az oldat hígításával nő.
A pH az összes hidrogénion koncentrációtól függ. Az első disszociációs lépcső teljes, így az ebből eredő [H+]=0,003 M. Ez a kezdeti koncentráció a második lépcső számára, amely az egyensúly szerint változtatja a koncentrációkat:
| HSO4-+ | H2O Ű | SO42- | + H3O+ | |
| K: | 0,003 | 0 | 0,003 | |
| R: | -y | y | y | |
| E: | 0,003-y | y | 0,003+y |
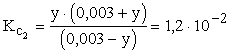 , melyből
, melyből ![]()
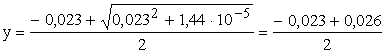
y1 = 1,5·10-3
Az egyenlet második gyökének (negatív érték!) nincs értelme, ezért eltekintünk tőle.
[H3O+] = 3·10-3 + 2,37·10-3 = 5,37·10-3 M. pH = 2,27
Ha ezt az eredményt összehasonlítjuk a 44. feladat eredményével (pH = 2,22), az eltérés nem túl nagy, de jelentős. Oldjuk meg a 60. feladatot!
Az első lépésre:
| H2S + | H2O Ű | HS- + | H3O+ | |
| K: | 0,1 | 0 | 0 | |
| R: | -x | x | x | |
| E: | 0,1-x | x | x |
A második lépcsőre:
| HS- + | H2O Ű | S2- + | H3O+ | |
| K: | x | 0 | x | |
| R: | -y | y | y | |
| E: | x-y | y | x+y |
A komponensek koncentrációi:
[H2S] = 0,1 - x; [HS-] = x - y; [S2-] = y; [H3O+]
= x + y
Az egyensúlyi állandók kifejezései:
![]()
![]()
A K értékek alapján arra következtethetünk, hogy x » y. Ezért
![]()
Ezt behelyettesítve a következő kifejezést kapjuk:
![]()
és ![]()
A H2S nagyon gyenge sav és feltételezhetjük, hogy az első disszociáció
5%-nál kisebb, ezért (0,1-x) × 0,1:
![]()
ezért x2 = 1,1·10-8; x = 1·10-4; y = 1·10-14
Végül az egyensúlyi koncentrációk:
[H2S] = 0,1 M
[HS-] = 1·10-4 M
[S2-] = 1·10-14 M
[H3O+] = 1·10-4 M, pH = 4
Az alkalmazott számítási módszer ugyanaz, mint amit az előző feladatnál
használtunk. Hasonlóan alkalmazva x és y jeleket, azt a következtetést vonhatjuk le,
hogy a koncentrációk:
[H2CO3] = I - x
[HCO3-]= x - y
[CO32-] = y
[H3O+] = x + y = 3,02·10-6 (pH = 5,52-ből számítva)
ahol I a kezdeti H2CO3 koncentrációt jelenti. Mivel
![]() »
»
![]() , ezért (x-y)
@ (x+y) @ x. Először is tételezzük fel, hogy I » x, ezért
, ezért (x-y)
@ (x+y) @ x. Először is tételezzük fel, hogy I » x, ezért
![]()
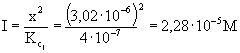
Az eredmény azt bizonyítja, hogy "x" nem hanyagolható el "I"
mellett:
![]()
így I =x2/![]() + x = 2,28·10-5 + 3,02·10-6 = 2,58·10-5 M
+ x = 2,28·10-5 + 3,02·10-6 = 2,58·10-5 M
Megjegyzés
Az eredmény talán félrevezető, mert azt sugallja, hogy az első disszociáció nagyon csekély.
értéke azonban azon a feltételezésen alapul, hogy az összes CO2 molekula oldott állapotban, H2CO3 formájában szerepel. Valójában a CO2 és H2CO3 egyensúlyban vannak:
azaz 480 CO2 molekula közül csak egyetlenegy van H2CO3 formájában, a többi szén-dioxid marad.
A használt
értéke az alábbi reakcióra vonatkozik:
CO2 + 2 H2O Ű HCO3- + H3O+
és nem a következőre:
H2CO3 + H2O Ű HCO3- + H3O+
ezért [CO2] az oldott CO2 összkoncentrációja.
megadott értéke egy "látszólagos" disszociáció állandónak felel meg. Minthogy [CO2] értéke jóval nagyobb, mint [H2CO3], a "valódi" disszociáció állandó nagyobb, mint a megadott érték.
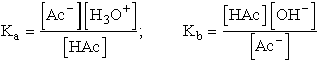
ahol "HAc" és "Ac" ecetsavat, ill. acetátiont jelent. A két kifejezést összeszorozva a víz ionszorzatát nyerjük
Ka . Kb = Kv
Ez az összefüggés mindig igaz konjugált sav-bázis párokra.
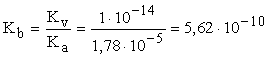
A nátrium-acetát, CH3COONa teljes mértékben disszociáló só, így oldatban Na+ és CH3COO--ionokat ad. A Na+-ion mint rendkívül gyenge sav lényegtelen tényező, az acetátion disszociációs egyensúlyát az előző feladat alapján kell számolni.
- Ha Kb ismert:
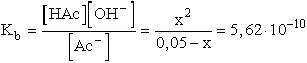
Az egyenletet megoldva, x = [OH-] = 5,3.10-6, pH = 8,72
- Ha Kb-t nem ismerjük, használjuk a Kb és Ka közötti összefüggést, így Kb értékét ki tudjuk számítani.
A nátrium-hidroxid, erős bázis, az ecetsavval nátrium-acetát képződése közben reagál. Ez a só teljes mértékben disszociál és Na+, ill. Ac- ionokat ad. Az Ac- ionok részlegesen hidrolizálnak és részt vesznek a hidrolitikus egyensúlyban. Először számítsuk ki az új koncentrációkat (az elegy térfogata 200 cm3 lett!):
[NaAc] = 0,05 M
[NaOH] = 0 M
[HAc] = 0,1 M
Ezután számítsuk ki az egyensúlyi koncentrációkat:
| HAc + | H2O Ű | Ac- + | H3O+ | |
| K: | 0,1 | 0,05 | 0 | |
| R: | -x | x | x | |
| E: | 0,1-x | 0,05-x | x |
![]()
x2 + (0,05 + Kc)x + 0,1·Kc = 0
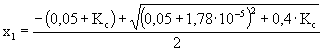
x = 3,64.10-5 pH = 4,43
Meggondolva, hogy a HAc gyenge sav disszociációja a "külső" acetátionok
hatására még kisebb lesz, azt az egyszerűsítést tehetjük, hogy
(0,05 + x) @ 0,05
(0,1 - x) @ 1
ezért ![]()
![]()
pH = 4,45, tehát a feltételezés helytálló.
- Alkalmazzuk a már megtárgyalt közelítést:
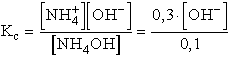
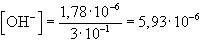
pH = 8,77
- Higítás után az új koncentrációk
[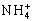 ] = 0,03 M és
] = 0,03 M és
[OH-] = 0,01 M lesznek.
Behelyettesítve ezeket az értékeket a kifejezésbe, az eredmények változatlanok maradnak.
- Az eredeti pufferoldat pH-ja:
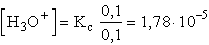
pH = 4,75
- A pufferoldathoz adott sav után a HCl koncentrációja:
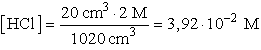
A puffer koncentrációváltozása 20 cm3 térfogatnövekedés miatt elhanyagolható lenne, azonban a H3O+ hozzáadott mennyisége reagál az acetátionokkal és ecetsavat képez. Ezért az acetátionok és az ecetsav mennyisége megváltozik:
[Ac-] = [só] - [HCl]
[HAc] = [sav] + [HCl]
Fentieket figyelembevéve:
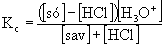
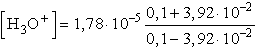
[H3O+] = 4,07.10-5, pH = 4,39
Puffer alkalmazása nélkül, egy 3,92·10-2 M koncentrációjú vizes oldat pH-ja: 1,41 lenne.
Az új koncentrációk:

| HAc + | H2O Ű | Ac- + | H3O+ | |
| K: | 9,52·10-2 | 0 | 4,76·10-2 | |
| R: | -x | x | x | |
| E: | 9,52·10-2 - x | x | 4,76·10-2 + x |
![]()
![]()
Tételezzük fel, hogy "x" kis érték, ezért elhanyagolható.
![]()
![]()
Az eredmény igazolja feltevésünket. A pH értékét kiszámíthatjuk, ha csak a sósav
oldat koncentrációját vesszük figyelembe:
[H3O+] = 4,76·10-2, pH = 1,32
Az új koncentrációk
[HCl] = 4,76·10-4 M
[HAc] = 9,52·10-2 M
Összehasonlítva ezt a feladatot az előzővel, az egyetlen eltérés, hogy a HCl koncentrációja most 2 nagyságrenddel kisebb, mint az előző feladat esetében.
| HAc + | H2O Ű | Ac- + | H3O+ | |
| K: | 9,52·10-2 | 0 | 4,76·10-4 | |
| R: | -x | x | x | |
| E: | 9,52·10-2 - x | x | 4,76·10-4 + x |
![]()
Az "x" elhanyagolható, de csakis a nevezőben:
![]()
x2 + 4,76.10-4 . x - 1,695.10-6 = 0
![]()
x = 1,085.10-3
[H3O+] = 1,085·10-3 + 4,76·10-4 = 1,561·10-3
M
pH = 2,81
a) 0,7 CH3COOH - 1 CH3COONa
b) 3,9 NH4OH - 1 NH4Cl
c) 0,5 NH4OH - 1 NH4Cl
Az AgI disszociációja:
| AgI Ű | Ag+ | + I- | |
| K: | - | 0 | 0 |
| R: | - | x | x |
| E: | - |
x | x |
Az ezüst-jodid oldhatósági szorzata, L = 1,5·10-16. Behelyettesítve az
oldhatósági szorzat kifejezésbe
L = x2
![]()
Ha a Pb2+ ionok koncentrációja x, akkor a I- ionoké 2x. Behelyettesítve ezeket az oldhatósági szorzat kifejezésbe:
L = 8,7·10-9 = [Pb2+][I-]2 = x(2x)2 = 4 x3
és ez a PbI2 oldhatósága is.
- L = x2 x = [Ag+]= [AgCl]
S = 1,27× 10-5 M - Közös a Cl- ion. A HCl disszociációjából származó nagy mennyiségű
Cl- ion fog dominálni, azaz:
L = [Ag+]·0,1
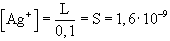
- A HNO3-ban nincs közös ion, ezért első közelítésben az oldhatóság
nem változik.
- Az ammónium-hidroxid az AgCl csapadékot a következő reakcióegyenlet szerint oldja:
Ag+ + 2 NH3 = [Ag(NH3)2]+ (a)
az oldhatósággal kombinálva:
AgCl = Ag+ + Cl- (b)
Az (a) és (b) egyenleteket összeadva:
AgCl + 2 NH3 Ű [Ag(NH3)2]+ + Cl- (c) K: 1,0 0 0 R: -2x x x E: 1,0-2x x x A (c) egyenlet egyensúlyi állandóját Kc·L szorzatként kapjuk:
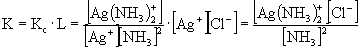
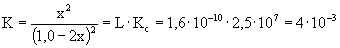
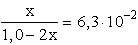
x = S = 5,6· 10-2 mol/l
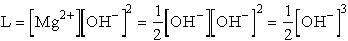
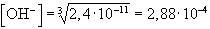
pH = 10,46
- pH = 11, ezért [OH-] = 10-3 M, ezt L-be helyettesítve:
L = [Mg2+][10-3]2
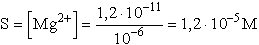
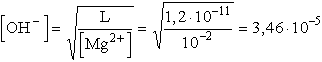
pH = 9,54
![]()

A 61. feladatban szereplő közelítéseket értelemszerűen itt is használtuk.
x = 1,1·10-8 M
y = [S2-] = 1,1·10-22 M
Az oldhatósági szorzatba helyettesítve:
LCuS = [Cu2+][S2-] = [Cu2+]·1,1·10-22
= 6·10-36
LZnS = [Zn2+][S2-] = [Zn2+]·1,1·10-22
= 3·10-22
Fentiekből az oldhatóság kifejezhető:
SCuS = [CuS] = [Cu2+] = 5,45·10-14 M és
SZnS = [ZnS] = [Zn2+] = 2,73 M
Az eredményekből arra következtethetünk, hogy 0,1 M HCl oldat jelenlétében a CuS leválik, a ZnS azonban nem (leválásakor azonnal feloldódik).
FeS: [S2-] = 6·10-15
MnS: [S2-] = 1,4·10-12
Előbb az FeS válik le.
[S2-] = 1,1·10-22, [Hg2+] = 4·10-53/1,1·10-22.
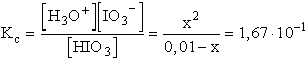
Ebből
x = 0,00945
Behelyettesítve
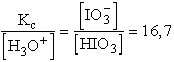
Amint látható az ![]() ionok jelentos része nem disszociált formában van jelen. Mivel egyéb közös ion
nincs, az [Ag+] koncentrációjának egyenlőnek kellene lenni az összes
ionok jelentos része nem disszociált formában van jelen. Mivel egyéb közös ion
nincs, az [Ag+] koncentrációjának egyenlőnek kellene lenni az összes ![]() koncentrációval
tekintet nélkül arra, hogy az disszociált, vagy nem disszociált formában van jelen:
koncentrációval
tekintet nélkül arra, hogy az disszociált, vagy nem disszociált formában van jelen:
[Ag+] = ![]() + [HIO3]
+ [HIO3]
[HIO3] kifejezhető mint:
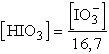
![]() -ba
behelyettesítve, a következő kifejezés írható fel:
-ba
behelyettesítve, a következő kifejezés írható fel:
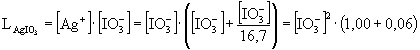
![]() = 9,3·10-5 M; [HIO3]
= 5,6·10-6 M és S = [Ag+] = 9,87·10-5 M
= 9,3·10-5 M; [HIO3]
= 5,6·10-6 M és S = [Ag+] = 9,87·10-5 M
| PbCl2 Ű | Pb2+ + | 2 Cl- | |
| E: | x | 2x | |
| PbI2Ű | Pb2+ + | 2I- | |
| E: | y | 2y |
A teljes Pb2+ koncentráció:
[Pb2+] = x + y
Az oldhatósági szorzatok:
L1 = [Pb2+][Cl-]2 = (x + y)(2x)2
L2 = [Pb2+][I-]2 = (x + y)(2y)2
x és y aránya kiszámítható:
![]()
ebből y = 0,03x.
Ezt az oldhatósági szorzatok kifejezéseibe helyettesítve:
1,03x4x2 = 1,6·10-5
x3 = 3,887·10-6
x = [PbCl2] = 1,57·10-2 M
y = [PbI2] = 4,72·10-4 M