A termodinamika az energiaváltozást vizsgáló tudomány. A természetben minden kémiai folyamatot és fizikai változást a termodinamika törvényei irányítanak és ebből a szempontból nem teszünk különbséget kémiai és fizikai változás között. Vizsgálataink során a világegyetem speciális részére kell összpontosítanunk, ezt a részt rendszernek nevezzük. A rendszer lehet egy pohár víz, egy mozdony, egy O2 molekula, egy hallgatókkal teli előadóterem stb. Mindent, ami a rendszeren kívül van (és ez a világegyetem többi része), a környezetnek tekintjük és úgy is nevezzük. A rendszer különféle módon érintkezhet a környezettel. Ez lehet energia, ill. anyag leadása és felvétele.
Ha zárt a rendszer, akkor az anyag felvétele, leadása (anyagtranszport) a környezet felé tiltott, de energialeadás, ill. felvétel lehetséges.
Ha utóbbi sem lehetséges, akkor a rendszert elszigeteltnek vagy izoláltnak nevezzük.
A termodinamika első főtétele
A termodinamika első főtétele az energiamegmaradás törvényének kifejezése az alábbi egyenlet szerint:
DE = Q + W (1)
azaz, egy adott rendszer energiája kétféle módon változhat, munka- (W) vagy hő- (Q) átadással.
A termodinamikában a rendszer belső energiája (U) a teljes belső energiakészlete (a rendszer részeinek mozgási és kölcsönhatási energiája) így ehhez nem tartozik hozzá az egész rendszer helyzeti és mozgási energiája. Az energia az anyag velejáró tulajdonsága (ugyanúgy, mint a tömeg). Általában egy folyamatra nézve az abszolút belső energiákat nem nem számítjuk ki, csak az energiakülönbséget, DU-t. Praktikus értelemben ez nem jelent gondot, mivel számunka a belső energia megváltozása érdekes, nem pedig maga az abszolút energia.
DU = Uvégső - Ukezdeti (2)
A munka kifejezés a hő kivételével az energiaátmenet minden fajtáját magában foglalja. Megegyezés szerint, ha a rendszer munkát végez, a munka negatív előjelű, ha a rendszeren végzünk munkát, munkát fektetünk be, akkor a munka előjele pozitív.
Egy különleges és gyakran használt munka, amely során egy gáz a külső nyomás ellen kiterjed (mint amikor egy gépkocsi motorjában a dugattyút a robbanás kifelé nyomja) az ún. térfogati munka:
W = -pDV (3)
ahol p a külső nyomás és DV a térfogatváltozás. Az előjel negatív, ha a vizsgált rendszer végez munkát (kiterjed), egyébként az előjel pozitív.
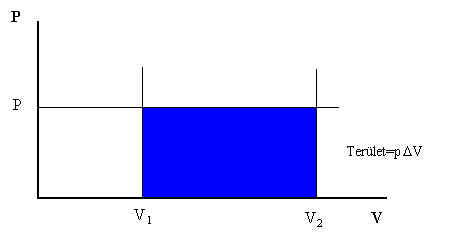
A térfogati munka legegyszerűbb ábrázolása a p-V diagramon (VIII.1. ábra) az árnyékolt területeken látható.

VIII.1. ábra
Meg kell jegyeznünk, hogy ha a térfogatváltozás alatt a nyomás nem állandó, a térfogati munka az alábbi integrállal adható meg:
![]() (4)
(4)
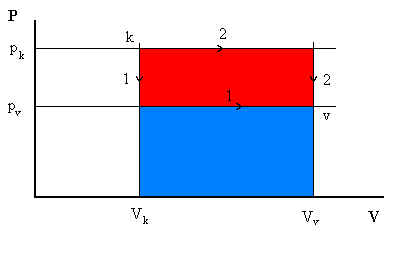
VIII.2. ábra
Vizsgáljunk meg egy folyamatot (energiaátvitel) a rendszer és környezete között és magyarázzuk a p-V diagram segítségével (VIII.2. ábra). A rendszer belső energiája a k(ezdeti) pontról a v(égső) pontra változott, DU1 = Uvégső - Ukezdeti. Nyilvánvaló, hogy ha a különböző munka- és hőmennyiségeket változtatjuk, k és v között különböző utak találhatók.
Az 1. út azt jelenti, hogy először a nyomás esik le pk-ről pv-re állandó térfogaton, majd állandó nyomáson változik a térfogat Vk-ről Vv-re. Nyilvánvaló, hogy az így végzett W1 = pv(Vv-Vk) sokkal kisebb, mint a 2-es úton végzett térfogati munka (melynek során először állandó pk nyomáson a térfogat változik Vk-ról Vv-re, majd állandó Vv térfogaton a nyomás pk-ról pv-re): W2 = pk(Vv-Vk).
Könnyű bizonyítani, hogy az energiaátmenet mindkét úton ugyanaz, DU1 = DU2. Tegyük fel, hogy ez nem igaz. Ebben az esetben a "2" úton visszafelé haladva (amikor az energia - DU2 értékkel változik), körfolyamatot létesíthetünk, és ha a két folyamatot egymást követően hajtjuk végre, a kezdeti állapotba kellene jutnunk. A teljes folyamat irányának megfelelően nyerhetünk és veszíthetünk energiát, ami természetesen ellentmond az energia megmaradásának. Ez az ellentmondás elkerülhető, ha feltételezzük, hogy egy körfolyamat összenergia változása nullával egyenlő. Ezért egy rendszer két állapotának energiaváltozása független az úttól.
Azokat a termodinamikai függvényeket, amelyek függetlenek az úttól, és csak a kezdeti és végállapottól függenek, állapotfüggvényeknek nevezzük. A belső energia állapotfüggvény.
DU1 és DU2 egyenlősége a példában szükségessé teszi, hogy a különböző értékű W1 és W2 munkamennyiségeket különböző Q1 és Q2 hővel ellensúlyozzuk. Következésképpen a hő és a munka nem állapotfüggvények, mivel a rendszer adott változásában eltérő értékeket vehetnek fel, amelyek a megtett úttól függenek (útfüggvények). Ezeket a mennyiségeket állapotváltozóknak nevezzük.
A hő áramlása hőmérsékletkülönbség hatására bekövetkező energiaátvitel; a hő mindig melegebb területekről áramlik a hidegebb felé. Ha egy rendszerrel hőt közlünk, a rendszer hőmérséklete (az úttól függően) általában emelkedik. A hőmérséklet változása a közölt hő mennyiségével egyenesen arányos.
Q = C ˇ DT (5)
A C állandót a rendszer hőkapacitásának nevezik. C értéke a rendszer tömegétől függ, egy nagytömegű test azonos hőmérsékletre történő emelése több hőt igényel, mint egy kicsié. Ezért célszerű egységnyi tömegű test hőkapacitásáról beszélni. Így vezetjük be a moláris hőkapacitás Cm fogalmát, amely egy mol anyag hőkapacitása. Hasonló módon 1 gramm anyag hőkapacitását fajhőnek nevezzük és c-vel jelöljük, ennek felhasználásával az (5) egyenlet az alábbiakban fejezhető ki:
Q = Cm ˇ n ˇ DT (6a)
Q = c ˇ m ˇ DT (6b)
ahol "n" és "m" az anyagmennyiség molban, ill. grammban.
Ha vasfazekat égő tűzhelyre helyezünk, akkor a hőmérséklete a tűzhely által leadott hőnek megfelelően emelkedni fog. Ha a vas tömegével egyenlő tömegű vizet helyezünk a fazékban a tűzre, a víz hőmérséklete lassabban fog emelkedni. Valójában több mint kétszer olyan hosszú ideig tart, amíg a fazéknyi vizet felmelegítjük, mint a fazekat üresen.
Hogy adott hőmérsékletre melegítsük, a vas kevesebb hőt igényel, mint ugyanolyan tömegű víz. Más oldalról tekintve, adott hő magasabb hőmérsékletre melegíti a tömegegységnyi vasat, mint a vizet.
A fajhő és a moláris hőkapacitás tehát az anyag fontos jellemzői.
A hőkapacitás azoktól az állapothatározóktól is függ, amely(ek)en a hőt a rendszerrel közöltük. A VIII.3. ábrán néhány különböző út látható a p-V diagramon ábrázolva. Ebben az esetben a rendszer egy gáz, melynek állapotát két izoterma szemlélteti. (Emlékezzünk a tökéletes gázok törvényére, pV = nRT). Az első úton a gázt állandó térfogaton T1-ről T2-re melegítjük, a második esetben a nyomás állandó. A harmadik út egy izoterma mentén végbemenő változás, amikor melegítés során a gázt úgy terjesztjük ki, hogy a kiterjedő gáz lehűlése kiegyenlítse a melegítést. Nyilvánvaló, hogy a hőkapacitás értéke különböző utakon más és más. Állandó nyomáson a gáznak térfogati munkát kell végeznie a külső nyomás ellenében, ezért az állandó nyomáshoz tartozó hőkapacitás érték nagyobb, mint az állandó térfogathoz tartozó. (Az állandó nyomás, ill. állandó térfogathoz tartozó hőkapacitás értékeket Cp, ill. Cv rövidítéssel jelöljük.)
VIII.3. ábra
A hőkapacitás a hőmérséklettől függ, ezért az (5) egyenlet helyett a számítás pontosabb módja integrálás lenne. Rendszerint azonban jó közelítéssel elhanyagolhatjuk a hőmérsékletfüggést, ha a hőmérsékletváltozás nem túl nagy.
Látens hő
A VIII.3. ábra harmadik útján a hőkapacitás végtelen nagy, minthogy az izoterma mentén a rendszer hőmérséklete nem változik annak ellenére, hogy hőt közöltünk vele. Hasonló jelenség észlelhető fázisátalakulások során. Ha egy 0 oC-os jég darabot melegítünk és az megolvad, az olvadás során a hőmérséklet nem változik. Amikor a jég teljesen megolvadt, a hőmérséklet emelkedni kezd. Ugyanez a jelenség figyelhető meg forrás, szublimáció és egyéb más fázisátalakulások során is; a folyamat közben a belső energia nagymértékben változik, a hőmérséklet növekedése nélkül. Tehát fázisátalakulások során a fajhő értéke végtelen naggyá válik.
Azt a befektetett hőmennyiséget, amely szükséges ahhoz, hogy egy gramm (egy mol) anyag az egyik fázisállapotból hőmérsékletnövekedés nélkül kerüljön át egy másik fázisállapotba, látens hőnek (moláris látens hőnek) nevezzük. Néhány fontos látens hő definícióját az alábbiakban adjuk meg:
moláris olvadáshő: az a hőmennyiség, amely 1 mol szilárd anyag megolvasztásához szükséges;
moláris fagyáshő: az a hőmennyiség, amely egy mol folyadék szilárd állapotba hozásához szükséges. A fagyáshő értéke megegyezik a moláris olvadáshő értékével, de annak ellenkező előjellel vett mennyisége;
moláris párolgáshő és kondenzációs hő: az a hőmennyiség, amely 1 mol folyékony halmazállapotú anyag elpárologtatásához, ill. 1 mol gőzhalmazállapotú anyag kondenzációjához szükséges. Szintén azonos értékű mennyiségek, de ellenkező előjellel.
moláris szublimációs hő: 1 mol szilárd anyag elpárologtatásához szükséges hőmennyiség. A moláris szublimációs hő a moláris olvadáshő és moláris párolgáshő összege, ha a fázisátalakulásnál a nyomás és a hőmérséklet értéke nem változik.
Entalpia
Ha egy rendszerben a térfogati munkán kívül más munka nem végződik (sem a rendszer nem végez munkát a környezetén, sem a környezet a rendszeren), az első főtétel szerint a belső energia kifejezhető a térfogati munka és az átadott hő összegével. Ha a térfogat a folyamat alatt állandó, akkor a hő egyenlő a belső energia megváltoztatásával:
Q = DU (7)
Az állandó nyomás feltétele azonban gyakoribb és sokkal könnyebben megvalósítható, mint az állandó térfogaté. Ezért bevezethetünk egy új termodinamikai állapotfüggvényt, az entalpia (H) fogalmát:
H = U + pV (8)
Csakúgy, mint a belső energiát, amely nem mérhető abszolút skálán, az entalpiát sem lehet közvetlenül mérni. Egy rendszer entalpiaváltozása azonban mérhető:
DH = DU + D(pV) (9)
Ha a nyomás állandó, azaz egy külső nyomással egyensúlyt tart, akkor
DH = DU + p DV (10)
DU értékét az első főtételből behelyettesítve azt kapjuk, hogy:
DH = Q - p DV + p DV = Q (11)
az entalpiaváltozás egyenlő az állandó nyomáson vett reakcióidővel.
Az előző példák alapján, ahol állandó nyomás volt a feltétel és csak térfogati munkavégzés történt, egyéb munkavégzés nem, a számított hőmennyiség mindig az entalpia végső és kezdeti állapota közötti különbség volt.
Kémiai reakciók entalpiaváltozása
A kémiai reakciók majdnem kivétel nélkül energiaelnyeléssel vagy felszabadulással járnak együtt. Az energia (vagy entalpia, mivel a kémiai reakciók általában állandó nyomáson játszódnak le) különböző formában fordulhatnak elő. Leggyakrabban a reakció során keletkező vagy elnyelt hőt észleljük, amely kaloriméteres kísérletek során egyszerűen mérhető.
A VI. fejezetben a kémiai reakcióegyenlet különböző jelentéseit tárgyaltuk meg. Egy kémiai reakció entalpiamérlegét tanulmányozva az egyenleteket új értelemmel gazdagíthatjuk. Az olyan reakcióegyenleteket, ahol a reakció során felvett vagy leadott hőt (entalpiamérleget) is jelöljük "termokémiai" egyenletnek nevezzük. Az alábbi példa azt szemlélteti, hogyan képez egy exoterm reakció során hidrogén és oxigén vizet.
a./ 2 H2(g) + O2(g) - 573,2 kJ = 2 H2O(f)
b./ 2 H2(g) + O2(g) = 2 H2O(f) + 573,2 kJ
c./ 2 H2(g) + O2(g) = 2 H2O(f) DH = -573,2 kJ
Mindhárom egyenlet ugyanazt fejezi ki: "Ha két mol hidrogén és egy mol oxigén két mol vizet képez, akkor 573,2 kJ hő keletkezik. A továbbiak során a "c" típusú egyenleteket fogjuk alkalmazni.
Ha hő nyelődik el, a végtermékek entalpiatartalma nagyobb, mint a reagáló anyagoké. Ezért a rendszer (ebben az esetben a reakcióedény) hőt vesz fel a környezetétől a reakció során, ebből következik, hogy DH előjele pozitív. A reakcióknak ezt a típusát "endoterm" reakciónak nevezzük.
A kémiai reakciókban végbemenő energiaváltozás mennyiségi vizsgálata megköveteli, hogy a halmazállapotot - gáz, folyadék, ill. szilárd fázis - megadjuk. A halmazállapotot minden képlet után zárójelben a megfelelő fázis kezdőbetűjével jelöljük. A jelet tehát, sz, f, g, melyek a szilárd, folyékony és gáz halmazállapotot jelölik. A vizes oldat jele: "aq" (aqua (latin) = víz). Rendszerint az a feltétel, hogy a reakció 25 oC-on és atmoszférikus nyomáson menjen végbe, az anyagok pedig "standard" állapotukban legyenek. (A reakcióhő függ a nyomástól és a hőmérséklettől.) A "standard" állapot az anyag legstabilabb állapota a fent megadott állapothatározók mellett. Azaz a
C(sz) + O2(g) = CO2(g) DH = -393,5 kJ
reakcióban a szén standard állapota a grafit, az O2 és CO2 gázok 101 kPa nyomás mellett szerepelnek. A "standard" DH értékek táblázatokban találhatók meg.
Gyakorlati felhasználás céljára két speciális reakciótípust
érdemes megvizsgálni. Az első esetben egy mol vegyület képződik elemeiből. A
standard moláris entalpiát ilyen esetekben standard moláris képződési
entalpiának nevezzük, kevésbé pontosan, de igen gyakran képződéshőnek
nevezzük és ![]() -val
jelöljük.
-val
jelöljük.
Elfogadjuk azt a megállapodást, hogy minden elem képződéshője standard állapotban nullával egyenlő. A szervetlen és szerves anyagok standard moláris képződési entalpiák értékeit a 12-13. táblázatok adják meg.
Standard moláris égési entalpiának vagy égéshőnek
nevezzük egy reakció standard moláris entalpiáját (![]() ), ha egy mol anyagot oxigénfeleslegben
elégetünk. Megjegyezhető, hogy a fenti egyenlet DH értéke
egyszerre adja a szén standard moláris égési entalpiáját, valamint a szén-dioxid
standard moláris képződéshőjét.
), ha egy mol anyagot oxigénfeleslegben
elégetünk. Megjegyezhető, hogy a fenti egyenlet DH értéke
egyszerre adja a szén standard moláris égési entalpiáját, valamint a szén-dioxid
standard moláris képződéshőjét.
Amint említettük, az entalpia állapotfüggvény, ezért változása a rendszer kezdeti és végállapotától függ. A kémiai reakciók világában számos olyan folyamat van, amelyekre a DH-t közvetlenül meghatározni rendkívül körülményes vagy éppenséggel lehetetlen. Mégis, ezek az entalpiák egyszerű módon számíthatók, megtalálva a kerülőutat. Ezt a termokémiában "Hess-tételnek" nevezik. A Hess-tétel a termokémia alaptétele kimondja, hogy a kémiai reakciókban felszabaduló vagy elnyelt hő (a reakcióhő) csak a kiindulási anyagoktól és a végtermékektől és azok állapotától függ. Ez azt jelenti, hogy egy reakció entalpiaváltozása ugyanaz az érték, ha a reakciót egy vagy több lépésben tettük meg (független az úttól). Általánosan:
DH = DHa + DHb + DHc + ...... (12)
ahol a, b, c ... azokat az egyenleteket jelentik, amelyek összegeképpen a kívánt reakció reakcióegyenlete érhető el. Hess tételének értelmezésére egy egyszerű példa látható a VIII.4. ábrán. A szénnek széndioxiddá történő oxidációjára különféle utak tételezhetők fel, mint az az alábbiakban látható:
a. Cgrafit = C(g) DHa = +716,7 kJ
b. C(g) + O2(g) = CO2(g) DHb = -1110,2 kJ
c. Cgrafit + O2(g) = CO2(g) DHc = -393,5 kJ
d. Cgrafit + 1/2 O2(g) = CO(g) DHd = -110,5 kJ
e. CO(g) + 1/2 O2(g) = CO2(g) DHe = -283,0 kJ
f. C(g) + 1/2 O2(g) = CO(g) DHf = -827,2 kJ
továbbá néhány összefüggés a különböző utakhoz:
DHc = DHa + DHb (1. út)
DHc = DHd + DHe (2. út)
DHc = DHa + DHf + DHe (3. út)
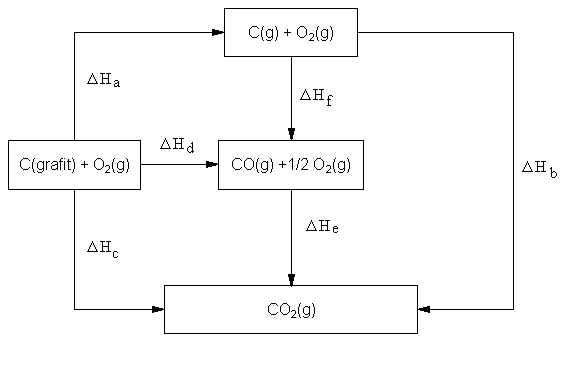
VIII.4 ábra
Grafit elégetésének különböző útjai
Látható, hogy a standard moláris képződési, ill. égési entalpiák hogyan használhatók fel: egy reakció úgy fogható fel, hogy a végtermékek standard moláris képződési (égési) entalpiának összegéből levonjuk a reagáló anyagok megfelelő standard entalpiáinak összegét:
![]() (13)
(13)
nt és nk a kérdéses reakcióegyenletben a résztvevő anyagok moljainak a száma.