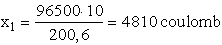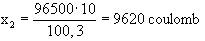- Megoldás:
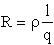 ,
ebből
,
ebből
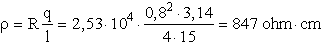
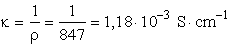
A 0,01 molos KCl oldat higítása cm3/mol
egységekben:
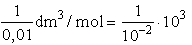 cm3/mol
= 105 cm3/mol
cm3/mol
= 105 cm3/mol
A molekulavezetés:
l =k j
= 1,18× 10-3×
105 = 118 S× cm2×
mol-1
- Megoldás:
A relatív ionmozgékonysági adatok alapján ki tudjuk számítani a hangyasav
oldat molekulavezetését végtelen nagy hígítás esetén:
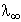 = lH+ + lHCOO-
= 349,7 + 55 = 404,7 S × cm2 ×
mol-1
= lH+ + lHCOO-
= 349,7 + 55 = 404,7 S × cm2 ×
mol-1
A disszociációfok:
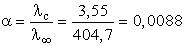 ,
,
tehát a disszociáció 0,88%-os.
- Megoldás:
A 4,2%-os oldat 100 g-ja 4,2 g KOH-t tartalmaz. A 100 g oldat térfogata:
 ml
ml
A KOH molekulatömege 56,1. Számítsuk ki, hány mol KOH van 1000 ml oldatban:
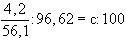
c = 0,768 mol/l
Számításainkban a koncentrációt mol/cm3-ben kell megadnunk:
c = 7,68 × 10-4 mol/cm3
A molekulavezetés és a koncentráció ismeretében ki tudjuk számítani
a fajlagos vezetést:
k = j c = 188,4×
7,68× 10-4 = 1,447×
10-1 S× cm-1
Az oldat ellenállása:
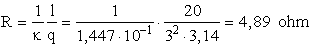
- Megoldás:
Az 1,67-es pH-jú ecetsav oldatban a hidrogénion koncentráció:
[H+] = 2,14× 10-2 mol/l.
Az ionmozgékonysági adatokból (lH+ = 349,7 S ×
cm2 × mol-1, lCH3COO-=
41 S × cm2 ×
mol-1) kiszámítjuk a végtelen hígításra extrapolált molekula-
vezetést:
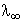 = 349,7 + 41 = 390,7
S × cm2 × mol-1
= 349,7 + 41 = 390,7
S × cm2 × mol-1
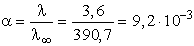
A hidrogénion koncentráció a totál koncentráció és a disszociációfok szorzata,
így
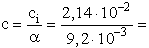 2,32 mol/l = 2,32× 10-3 mol/ml
2,32 mol/l = 2,32× 10-3 mol/ml
Minthogy 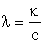 ,
a fajlagos vezetés:
,
a fajlagos vezetés:
k = l c = 3,6×
2,32× 10-3 = 8,35 ×
10-3 S× cm-1
A fajlagos ellenállás a fajlagos vezetés reciproka:
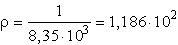 ohm× cm
ohm× cm
- Megoldás:
Az eloző példában már kiszámítottuk a relatív ionmozgékonysági adatok
alapján, hogy ecetsav esetén 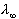 = 390,7 S × cm2
× mol-1. A 0,01 mol/l oldat higítása:
= 390,7 S × cm2
× mol-1. A 0,01 mol/l oldat higítása:
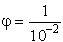 l/mol = 102× 103 ml/mol = 105 ml/mol
l/mol = 102× 103 ml/mol = 105 ml/mol
A molekulavezetés:
l = k j
= 1,63× 10-4×
105 = 16,3
Számítsuk ki a disszociációfokot:
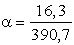 = 4,17× 10-2
= 4,17× 10-2
A hidrogénion koncentráció:
ci = [H+] = ca = 10-2× 4,17× 10-4
mol/l
A pH értéke:
-lg 4,17× 10-4 = -(0,622 - 4) = 3,378
A disszociációs egyensúlyi állandó a következő képlet alapján számolható:
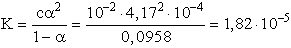
- Megoldás:
A relatív ionmozgékonyságok értéke:
lAg+ = 61,9 S× cm2× mol-1
lCl- = 76,32 S×
cm2× mol-1
A két relatív ionmozgékonyság összege a végtelen higításra extrapolált
molekulavezetést adja meg:
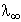 =
138,22 S× cm-2× mol-1
=
138,22 S× cm-2× mol-1
Az oldhatósági szorzat alapján kiszámítjuk a telített AgCl oldat koncentrációját:
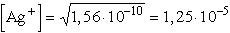 mol/l
mol/l
Az ezüstion koncenctráció megegyezik az oldatban levő AgCl koncentrációval
(teljes disszociáció):
c = 1,25× 10-5 mol/l = 1,25×
10-8 mol/cm3
A végtelen híg oldatban
k = 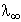 c = 138,22× 1,25×
10-8 = 1,73× 10-6 S×
cm-1
c = 138,22× 1,25×
10-8 = 1,73× 10-6 S×
cm-1
A fajlagos ellenállás:
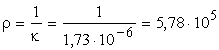 ohm× cm
ohm× cm
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
A Cu/Cu2+ rendszer normál elektródpotenciálja +0,34 V, a
Zn/Zn2+ rendszeré 0,76 V. Két redoxrendszer egymásra hatásakor
a pozitívabb elektródpotenciálú szerepel oxidálószerként, így a fenti reakció
balról jobbra megy önként végbe (E0 pozitív, tehát D
G0 negatív). A két elektródpotenciál különbsége 1,10 V. Az elektronszám
változás 2.
log K = 16,95× 2×
1,10 = 37,29
K = 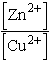 = 1,95× 1037
= 1,95× 1037
Az egyensúlyi állandó felírásánál figyelembe vettük, hogy a tiszta szilárd
anyagok aktivitása egységnyi.
Egyensúly esetén a Zn2+ ionok aktivitása 1,95 ×
1037-szerese a Cu2+ ionok aktivitásának.
Nem meglepő tehát, hogy fém Zn-t adva rézionok oldatához, a Cu2+
ionok gyakorlatilag teljes redukciója megy végbe.
Ha [Zn2+]/[Cu2+] arány nagyobb 1,95 ×
1037-nél, ellentétes irányú reakció játszódik le mindaddig, amíg
az egyensúly be nem áll. Az ellentétes irányú reakció egyensúlyi állandója
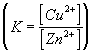 természetesen
a balról jobbra végbemenő folyamat egyensúlyi állandójának reciproka (példánkban
természetesen
a balról jobbra végbemenő folyamat egyensúlyi állandójának reciproka (példánkban
 = 5,12
× 10-38). Az egyensúlyi állandó részletesebben
is levezethető abból a megfontolásból, hogy egyensúly esetén a két elektródpotenciál
értéke megegyezik:
= 5,12
× 10-38). Az egyensúlyi állandó részletesebben
is levezethető abból a megfontolásból, hogy egyensúly esetén a két elektródpotenciál
értéke megegyezik:
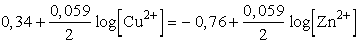
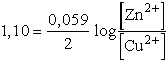
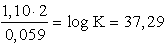
- Megoldás:
Két normál elektródpotenciál ismerete szükséges a megoldáshoz. A Cu/Cu+rendszer
normál elektródpotenciálja +0,52 V, a Cu+/Cu2+rendszeré
+0,153 V. Számítsuk ki először a felső nyíl irányába végbemenő folyamat
egyensúlyi állandóját annak alapján, hogy egyensúly esetén a két redox elektródpotenciál
megegyezik.
A folyamat a következő galvánelemben játszódik le:
Pt | Cu+, Cu2+ | Cu+ | Cu
A két elektródpotenciált egyenlővé téve:
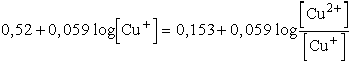 ,
,
ebből
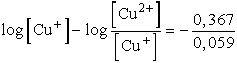
vagyis
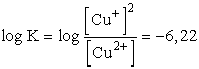
K = 6,03× 10-7
Az egyensúlyi állandó kiszámítható a log K = 16,95 zE0 képlettel
is, ha figyelembe vesszük, hogy a fenti reakcióirány a redoxpotenciálok
alapján várható reakcióirány ellentettjének felel meg, az E0
értéke tehát negatív (E0 = 0,153 - 0,52 = -0,367)
log K = -16,95 × 1 ×
0,367 = -6,22
- Megoldás:
Az Ag/Ag+ rendszer normál elektródpotenciálja 0,80 V, a Zn/Zn2+
rendszeré pedig -0,76 V
Az AgNO3 oldatba merülő ezüstelektród potenciálja a normál hidrogénelektródhoz
viszonyítva:
e Ag = e0
+ 0,059 log 0,27 = 0,80 + 0,059 (0,431 - 1) = 0,767 V
Ugyanígy számítható ki a cinkelektród potenciálja:
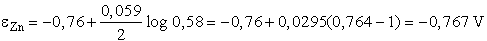
A galvánelem elektromotoros ereje:
E = e Ag + e
Zn = 0,767 - (-0,767) = 1,534 V
- Megoldás:
A feladat megoldásához ismerjük az ólomelektród normálpotenciálját (-0,13
V), a klórgázelektród normálpotenciálját (+1,36 V) és a Pb(OH)2 oldhatósági
szorzatát (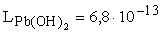 ).
Az oldhatósági szorzatból kiszámíthatjuk a negatív elektród környezetében
levő Pb2+ koncentrációt:
).
Az oldhatósági szorzatból kiszámíthatjuk a negatív elektród környezetében
levő Pb2+ koncentrációt:
L = 6,8× 10-13 = [Pb2+]
[OH-]2 = 4 [Pb2+]3
[Pb2+] = 5,5× 10-5 M
A pozitív elektród környezetében a Cl- koncentráció megegyezik
a H+ koncentrációval, vagyis a Cl- koncentráció negatív
logaritmusa (pCl) azonos a pH-val.
A Cl- koncentrációját nem is kell kiszámítani, minthogy a pozitív
elektród potenciáljának koncentrációtól függő része tartalmazza a Cl-
koncentráció negatív logaritmusát.
Az elektromotoros erő:
E = 1,36 - 0,059 log[Cl-] - (-0,13 + 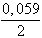 log[Pb2+] =
log[Pb2+] =
= 1,36 + 0,059× 3,3 + 0,13 - 0,0295 log 5,5×
10-5 = 1,575 V.
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
Valamely redoxrendszer oxidálóképessége annál nagyobb, minél pozitívabb
az elektródpotenciálja. A Cr3+/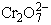 rendszer normál elektródpotenciálja +1,36
V. A fenti egyenlet átrendezésével:
rendszer normál elektródpotenciálja +1,36
V. A fenti egyenlet átrendezésével:
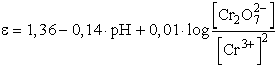
Így pH = 0 esetben
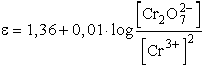
Tételezzük fel, hogy a 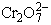 és a Cr3+ ionok aktivitása az egységhez közeli
érték. Erősen savas közegben tehát a halogenidionok közül a bromid és a
jodid egyértelműen halogénné oxidálható dikromáttal; a megfelelő redoxi
normálpotenciálok ugyanis: +2,85 V (F- Ű 1/2 F2), +1,36 V (Cl- Ű 1/2 Cl2), +1,07 (Br- Ű 1/2 Br2), +0,54 V (I- Ű 1/2 I2).
és a Cr3+ ionok aktivitása az egységhez közeli
érték. Erősen savas közegben tehát a halogenidionok közül a bromid és a
jodid egyértelműen halogénné oxidálható dikromáttal; a megfelelő redoxi
normálpotenciálok ugyanis: +2,85 V (F- Ű 1/2 F2), +1,36 V (Cl- Ű 1/2 Cl2), +1,07 (Br- Ű 1/2 Br2), +0,54 V (I- Ű 1/2 I2).
Ha pH = 3, akkor
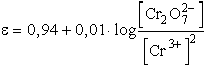
vagyis gyengén savas közegben a halogenidionok közül már csak a jodidot
oxidálja a dikromát.
- Megoldás:
Az Sn2+/Sn4+ redoxrendszer normálpotenciálja +0,15
V, az Fe2+/Fe3+ rendszeré +0,76 V. Kiszámítjuk az
egyes összetevők koncentrációját:
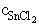 = 2,64×
10-3 M
= 2,64×
10-3 M 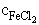 = 3,95× 10-4 M
= 3,95× 10-4 M
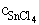 = 1,15×
10-2 M
= 1,15×
10-2 M 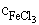 = 1,23× 10-2 M
= 1,23× 10-2 M
A galvánelem egyik sarkának elektródpotenciálját az Fe2+/Fe3+
redoxrendszer határozza meg:
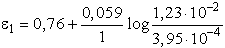 = 0,76 + 0,088 = 0,848 V
= 0,76 + 0,088 = 0,848 V
A másik elektród potenciálja:
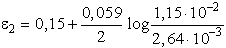 = 0,15 + 0,019 = 0,169 V
= 0,15 + 0,019 = 0,169 V
e 1 nagyobb pozitív érték, ez lesz
a galvánelem pozitív elektródjának potenciálja, és minthogy a pozitívabb
elektródpotenciálú redoxrendszer oxidálja a negatívabb elektródpotenciálút,
a galvánelemben a következő kémiai reakció megy végbe:
2 FeCl3 + SnCl2 <=> 2 FeCl2 + SnCl4
Ez a felírás megfelel az ismertetett egyenletfelírási konvenciónak, a reakció
a jobboldal irányába indul meg. A galvánelem elektromotoros ereje a két
elektród-potenciál különbsége: E = e 1
- e 2 = 0,679 V.
- Megoldás:
Erre a reakcióra az általános Nernst-egyenlet:
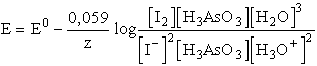
e0 a H3AsO3
+ 3 H2O <=>
H3AsO4 + 2 H3O+ + 2e rendszerre
+0,574 V,
e0 a 2 I- <=> I2 + 2e rendszerre +0,54
V.
E0 = 0,034 V
A teljes reakcióban 2 elektron megy át a 2 I--ról a H3AsO4-re,
így z = 2.
A tiszta anyagok aktivitása általában egységnyi, így a I2 és
a H2O elhagyható a kifejezésből:
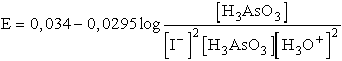
A komponensek egységnyi aktivitása esetén a tömeghatástört egységnyi, logaritmusa
zéró és az elektromotoros erő gyengén pozitív, így a körülmények a felső
nyíl irányába végbemenő reakciónak kedveznek. Ha azonban növeljük az oldat
pH-ját lúg hozzáadásával, [H3O+] értékének csökkenése
miatt E előjelt válthat. Semleges oldatban például [H3O+]
= 10-7, és feltételezve, hogy az összes többi komponens egységnyi
aktivitású, akkor
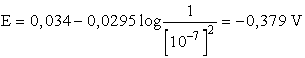
E negatív értéke azt jelzi, hogy a reakció a bal oldal irányába nem megy
végbe, hanem az ellentétes reakció játszódik le.
- Megoldás:
A Zn |Zn2+ ||Cd2+ | Cd
c = 0,01M c = 0,01 M
galvánelemben a
Zn + Cd2+ <=>
Zn2+ + Cd
reakció a felső nyíl irányában játszódik le, minthogy a Cd/Cd2+
rendszer normál elektródpotenciálja -0,40 V,
e 1 = -0,40 + 0,0295 log 10-2
= 0,459 V, és a
Zn/Zn2+ rendszer normál elektródpotenciálja -0,76 V;
e 1 = -0,76 + 0,0295 log 10-2
= 0,819 V,
vagyis a Cd elektród lesz a galvánelem pozitív pólusa. Ha azonban a Cd2+
ionokat tartalmazó oldatba KCN-t teszünk úgy, hogy a CN-
ion koncentráció 0,24 mol/l, a Cd2+ ionok a CN- ionokkal
[Cd(CN)4]2- komplex ionokat képeznek, az oldatban
levő Cd2+ ionok koncentrációját a komplex ion disszociációs egyensúlyából
számíthatjuk ki. Ezen disszociáció pK értéke (a disszociációs egyensúlyi
állandó negatív logaritmusa) 27,3.
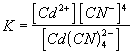
Kifejezhető a Cd2+ ionok koncentrációja:

A kis disszociációs egyensúlyi állandó miatt a disszociálatlan komplex ion
koncentrációja azonosnak vehető a totálkoncentrációval (a feleslegben levő
CN- ionok a disszociációt még vissza is szorítják), vagyis a
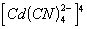 = 10-2
M.
= 10-2
M.
A feleslegben levő CN- ionok koncentrációja: 0,24 - 4×
0,01 = 0,2 M, így
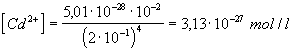
Ezen Cd2+ ion koncentráció esetén a Cd/Cd2+ rendszer
elektródpotenciálja:
e Cd = -0,40 + 0,0295 log 3,13×
10-27 = -0,40 - 0,782 = -1,182 V
A CN- ionok hatására tehát a Cd elektród lesz a negatív, ami
formálisan úgy fogható fel, hogy ilyen körülmények között a folyamat jobbról
balra megy végbe.
- Megoldás:
Az elektromotoros erő képletébe az aktivitásokat, tehát az ionkoncentráció
és aktivitási koefficiens szorzatokat helyettesítjük be.
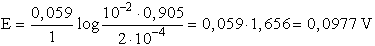
Az elem pozitív sarka a sósavoldatba merül, tekintettel arra, hogy ez a
töményebb oldat és pozitív ionok elektródfolyamatáról van szó.
- Megoldás:
A benzoesav gyenge sav, disszociációs egyensúlyi állandója 6,3×
10-5. Ebből kiszámítható a 0,05 molos benzoesav oldat hidrogénion
koncentrációja:
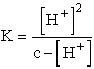 ,
6,3× 10-5 =
,
6,3× 10-5 = 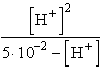 , [H+] = 1,796×
10-3 M
, [H+] = 1,796×
10-3 M
Minthogy ez a hidrogénion koncentráció kisebb, mint a HCl oldat hidrogénion
koncentrációja, a benzoesav oldatba merülő elektród lesz a galvánelem negatív
pólusa.
Az elektromotoros erő:
E = 0,059 log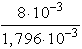 = 0,059 log 4,21 = 0,037 V
= 0,059 log 4,21 = 0,037 V
- Megoldás:
Az ammóniát tartalmazó AgNO3 oldatban az Ag+ ion
koncentrációja a komplexképződés miatt kisebb lesz, így az ebbe az oldatba
merülő elektród lesz a galvánelem negatív sarka. Kiszámítható ezen oldat
Ag+ koncentrációja az elektromotoros erő ismeretében:
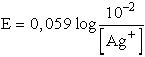
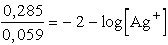
-log [Ag+] = 1,513× 10-7 M
A komplex disszociációs állandója:
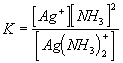
A kismértékű disszociáció miatt a komplex kation koncentrációja gyakorlatilag
azonos az oldatban levő AgNO3 koncentrációjával, 0,01 mol AgNO3
komplexbe viteléhez 0,02 mol NH3 szükséges, az egyensúlyi állandó
számlálójában szereplő NH3 koncentráció így 0,1-0,02 = 0,08 mol/l.
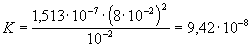
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
A higany atomtömege 200,6, 1 F hatására a higany(I)-bol 200,6 g,
a higany(II)-ből 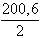 = 100,3 g választható le. Tehát 10 g higanynak higany(I)-nitrátból való
előállításához
= 100,3 g választható le. Tehát 10 g higanynak higany(I)-nitrátból való
előállításához
96500 : 200,6 = x1 : 10
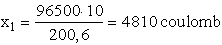
szükséges.
Ha ugyanezt a higanymennyiséget higany(II)-nitrátból kívánjuk előállítani,
akkor
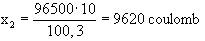
tehát kétszer akkora árammennyiségre van szükség.
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
- Megoldás:
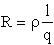 ,
ebből
,
ebből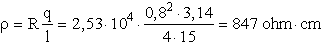
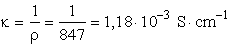
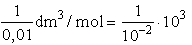 cm3/mol
= 105 cm3/mol
cm3/mol
= 105 cm3/mol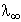 = lH+ + lHCOO-
= 349,7 + 55 = 404,7 S × cm2 ×
mol-1
= lH+ + lHCOO-
= 349,7 + 55 = 404,7 S × cm2 ×
mol-1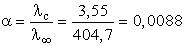 ,
, ml
ml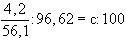
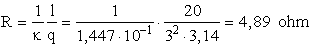
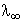 = 349,7 + 41 = 390,7
S × cm2 × mol-1
= 349,7 + 41 = 390,7
S × cm2 × mol-1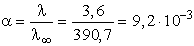
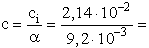 2,32 mol/l = 2,32× 10-3 mol/ml
2,32 mol/l = 2,32× 10-3 mol/ml 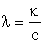 ,
a fajlagos vezetés:
,
a fajlagos vezetés: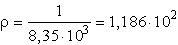 ohm× cm
ohm× cm
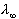 = 390,7 S × cm2
× mol-1. A 0,01 mol/l oldat higítása:
= 390,7 S × cm2
× mol-1. A 0,01 mol/l oldat higítása: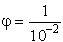 l/mol = 102× 103 ml/mol = 105 ml/mol
l/mol = 102× 103 ml/mol = 105 ml/mol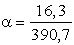 = 4,17× 10-2
= 4,17× 10-2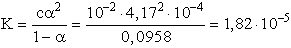
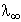 =
138,22 S× cm-2× mol-1
=
138,22 S× cm-2× mol-1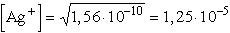 mol/l
mol/l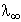 c = 138,22× 1,25×
10-8 = 1,73× 10-6 S×
cm-1
c = 138,22× 1,25×
10-8 = 1,73× 10-6 S×
cm-1 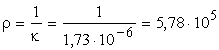 ohm× cm
ohm× cm
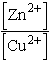 = 1,95× 1037
= 1,95× 1037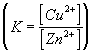 természetesen
a balról jobbra végbemenő folyamat egyensúlyi állandójának reciproka (példánkban
természetesen
a balról jobbra végbemenő folyamat egyensúlyi állandójának reciproka (példánkban
 = 5,12
× 10-38). Az egyensúlyi állandó részletesebben
is levezethető abból a megfontolásból, hogy egyensúly esetén a két elektródpotenciál
értéke megegyezik:
= 5,12
× 10-38). Az egyensúlyi állandó részletesebben
is levezethető abból a megfontolásból, hogy egyensúly esetén a két elektródpotenciál
értéke megegyezik: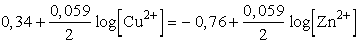
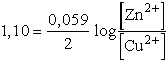
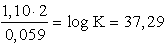
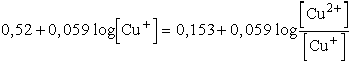 ,
, 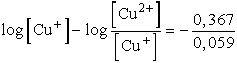
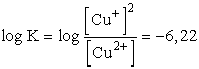
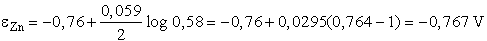
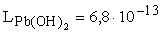 ).
Az oldhatósági szorzatból kiszámíthatjuk a negatív elektród környezetében
levő Pb2+ koncentrációt:
).
Az oldhatósági szorzatból kiszámíthatjuk a negatív elektród környezetében
levő Pb2+ koncentrációt: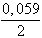 log[Pb2+] =
log[Pb2+] = 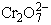 rendszer normál elektródpotenciálja +1,36
V. A fenti egyenlet átrendezésével:
rendszer normál elektródpotenciálja +1,36
V. A fenti egyenlet átrendezésével: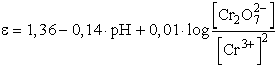
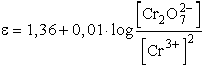
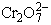 és a Cr3+ ionok aktivitása az egységhez közeli
érték. Erősen savas közegben tehát a halogenidionok közül a bromid és a
jodid egyértelműen halogénné oxidálható dikromáttal; a megfelelő redoxi
normálpotenciálok ugyanis: +2,85 V (F- Ű 1/2 F2), +1,36 V (Cl- Ű 1/2 Cl2), +1,07 (Br- Ű 1/2 Br2), +0,54 V (I- Ű 1/2 I2).
és a Cr3+ ionok aktivitása az egységhez közeli
érték. Erősen savas közegben tehát a halogenidionok közül a bromid és a
jodid egyértelműen halogénné oxidálható dikromáttal; a megfelelő redoxi
normálpotenciálok ugyanis: +2,85 V (F- Ű 1/2 F2), +1,36 V (Cl- Ű 1/2 Cl2), +1,07 (Br- Ű 1/2 Br2), +0,54 V (I- Ű 1/2 I2).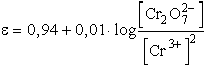
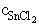 = 2,64×
10-3 M
= 2,64×
10-3 M 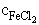 = 3,95× 10-4 M
= 3,95× 10-4 M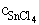 = 1,15×
10-2 M
= 1,15×
10-2 M 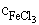 = 1,23× 10-2 M
= 1,23× 10-2 M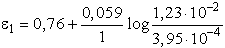 = 0,76 + 0,088 = 0,848 V
= 0,76 + 0,088 = 0,848 V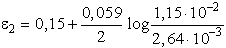 = 0,15 + 0,019 = 0,169 V
= 0,15 + 0,019 = 0,169 V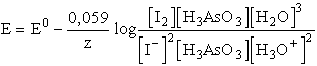
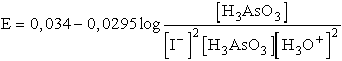
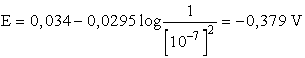
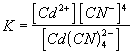

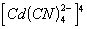 = 10-2
M.
= 10-2
M.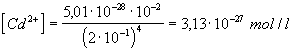
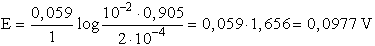
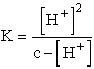 ,
6,3× 10-5 =
,
6,3× 10-5 = 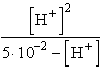 , [H+] = 1,796×
10-3 M
, [H+] = 1,796×
10-3 M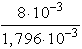 = 0,059 log 4,21 = 0,037 V
= 0,059 log 4,21 = 0,037 V
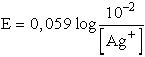
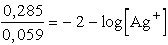
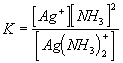
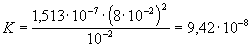
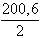 = 100,3 g választható le. Tehát 10 g higanynak higany(I)-nitrátból való
előállításához
= 100,3 g választható le. Tehát 10 g higanynak higany(I)-nitrátból való
előállításához