Density functional study of the relative stability of selected 1C4 and 4C1 chair forms of beta-D-glucose
Gábor I. Csonkaa, Krisztina Éliása and Imre G. Csizmadiab
aDepartment of Inorganic Chemistry, Technical University of Budapest, H-1521 Budapest, Hungary
bDepartment of Chemistry, University of Toronto, Toronto, Ontario, Canada M5S 1A1
Abstract
The method and basis set dependence of the relative energies of the 1C4 and 4C1 chair forms of beta-D-glucose were calculated for two selected, low energy hydroxyl rotamers at various levels of generalized gradient approximation density functional theory (GGA-DFT). The GGA-DFT and MP2 methods provide similar energetic differences for beta-D-glucose conformers. Addition of the diffuse functions to a double-zeta quality basis set and inclusion of the HF exchange into the DFT functionals improve the agreement between the DFT and the best composite estimates of the energetic differences. The GGA- or hybrid-DFT methods reproduce the geometrical consequences of correlation effects correctly for glucose. The extent of the correlation effects, however, varies with the applied functional. For C-C and C-O bond lengths the order is the following: r(HF) < r(B3P) < r(MP2) < r(B3LYP) < r(BP). The BP method shows the best agreement with the MP2 results for the bond angles. The difference between the ideal and calculated C-C-OH dihedral angles signals the strength of the O...H interactions. The inclusion of the electron correlation provides larger differences for the 4C1 conformers. For the 1C4 conformers the deviations are large because the repulsive eclipsing interactions of the OH groups with the ring C-C bonds is counterbalanced by the O...H interactions and nearly eclipsed rotamers occur. However, this effect is rather sensitive to the method and basis set. The inclusion of the diffuse functions into the basis set results in different rotamers.
This paper appears in Chem. Phys. Lett. (1996) without color figures and xyz coordinates. These coordinates can be processed by suitable plug-ins.
1. Introduction
Because of its biochemical importance D-glucose has been the subject of a series of recent theoretical studies [1]- [2] [3] [4] [5] [6] [7] [8] [9] [10]. These studies address questions related to the stability of hydroxyl and hydroxymethyl rotamers, the ring conformation, the structural and energetic consequences of anomeric effect, and solvation effects. Recent studies show a considerable agreement for the anomeric and solvation effects [3] [4] [6-8] [11], providing that the differential anomeric solvation effect is less than 1 kcal/mol.
Polavarapu and Ewig [4], as well as Schleyer and Salzner [8] showed for the hydroxymethyl rotamers of D-glucose, at HF/4-31G and 6-31G(d) levels of theory, respectively that the rotation of the exocyclic hydroxymethyl group has no influence on the energy difference between the alpha and beta anomers. The three-fold rotation of the four hydroxyl and the hydroxymethyl groups, in principle, can generate 36= 729 different rotamers.
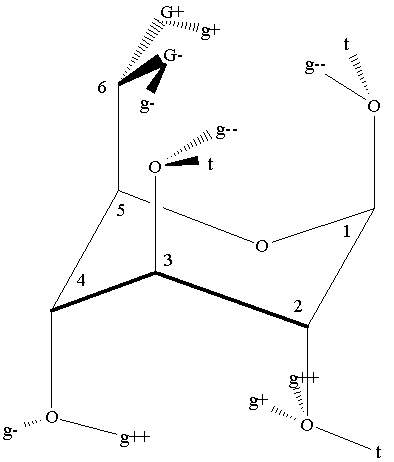
Figure 1. Schematic representation of some 1C4 and 4C1 chair hydroxyl and hydroxymethyl rotamers of beta-D-glucose. The idealized C(n+1)-C(n)-O-H torsions are denoted by g+, t and g- for gauche clockwise (60o), anti (180o), and gauche counterclockwise (-60o) respectively, where n = 1, 2, 3, 4. The idealized O5-C5-C6-O6 dihedral angles for the hydroxymethyl group are denoted by capital letters: G+, T, and G-. g++ or g-- notate torsions far from the idealized values for 1C4 chair conformer.
Figure 1 shows several rotamers of the 1C4 and 4C1conformers of beta-D-glucose using the notations of our previous paper [12]. Note that only the carbon atoms are numbered. These same numbers will be used to denote the oxygen atoms attached to those carbons throughout the paper. The idealized dihedral angles of the C(n+1)-C(n)-O(n)-H torsions, where n=1, 2, 3, 4 are designated by g+, t and g- for gauche clockwise (60o), anti (180o), and gauche counterclockwise (-60o), respectively. The idealized O5-C5-C6-O6 dihedral angles for the hydroxymethyl group are denoted by capital letters (G+, T, and G- as shown in figure 1).
NMR results for the rotamers of the hydroxymethyl group in the 4C1conformer of D-glucose provided that the G- and G+ rotamers were populated in about 55:45 ratio at room temperature, while the population of the T rotamer was negligible (less than 2%) [13]. In the crystal structure of the alpha-D-glucose [14] the G- orientation was found for the hydroxymethyl group. However, the crystal structure represents a conformer of considerably higher energy, by 8 kcal/mol at HF/6-31G(d) level of theory, because in this geometry the unfavorable orientations of the OH groups decrease the number of intramolecular hydrogen bridges [8]. At HF/6-31G(d) level of theory the G-g+ hydroxymethyl rotamer is the most stable, however, the differences between the three rotamers are below 0.2 kcal/mol [12]. At HF/4-31G level of theory the T rotamer is the most stable [4]. The inclusion of the Gibbs energy corrections stabilizes the G- rotamer, however, it becomes only slightly more stable (by 0.02 kcal/mol [4]) than the T rotamer. Barrows et al. [10] has showed recently that very large (cc-pVTZ or larger) basis set is required to get the correct energetic order for the hydroxymethyl rotamers at MP2 level of theory. Basis set extension corrections (up to cc-pVTQZ basis set) and correlation corrections (up to CCSD level) were also proposed.
The conformation of the aldopyranosyl ring is also an important issue. For the beta-D-glucopyranose it is well known that it takes an all-equatorial chair conformation, designated 4C1on figure 1. An alternative chair conformation, designated 1C4 on figure 1, puts all substituents in axial positions. Beside the correct description of various rotamers, the accurate modeling of the energetic and structural consequences of aldopyranose ring puckering is a challenging task even for the most advanced levels of theory. The results of Barrows et al. [10] show again that only very expensive MP2 calculations are able to reproduce the experimental energetic order. However, such calculations are clearly too demanding to become routine on a series of rotamers or conformers, or for larger oligosaccharides.
The primary focus of this letter is to find an economical alternative which can provide reliable energetic order and molecular geometry for glucopyranoses. These methods will be tested on further series of various hexapyranoses. The results of Barrows et al. [10] will be used as benchmark in this letter, thus we follow the selection of Barrows et al. [10]. The following codes identify the four selected conformers:
(1) 4C1 [t t t t G+ g-] |
(2) 4C1 [t t t t T g+] |
(3) 1C4 [t g+ g-- g- G+ g+] |
(4) 1C4 [g-- g++ g-- g++ G- g-] |
Where the order of the code letters follows the clockwise sequential numbers of the carbon atoms on figure 1, and g++ or g-- denotes further deviation compared to the idealized angles.
It
should be noted that the selection of the conformers by Barrows et al. [10] is somewhat
arbitrary. For example the 4C1 [t t t t G- g+]
conformation, which was not considered, is certainly very close in energy to the
conformers (1) and (2). This conformer is rather stable according the
experimental, HF and B3P/6-31G(d) results [12].
It is also possible that other rotamers might be equally or more stable than the conformers (3) and (4). However, our results show that some of the important features of the conformational space is well represented by these four conformers and they are suitable for benchmark purposes. The analysis of these structures leads to a better understanding of the real features of aldohexapyranose rings and the role of the electron correlation effects in the OH...O interactions.
2. Computational methods
We use the following combinations of the DFT functionals:
The geometries were optimized using the Berny algorithm combined with redundant internal coordinates built into the GAUSSIAN 94 program [21]. The DFT calculations were carried out using the sg1 (pruned to about 3000 points per atom) and fine (pruned to about 7000 points per atom) grids. The 6-31G(d), 6-31+G(d), 6-311G(d,p) [22], cc-pVDZ, aug-cc-pVDZ [23] basis sets were used. The calculations were performed on Silicon Graphics and IBM workstations.
3. Results and discussion
3.1. Relative energies
Earlier results, in Table 1, show that there is a monotonic change in the energetic order as the basis set quality increases at HF level of theory. The HF/3-21G results are inadequate for the energetic order because the HF/3-21G method over-stabilizes the 1C4 conformers relative to the 4C1conformers. The HF/6-31G(d) and cc-pVDZ results provide quite good relative energies that are close to the results of the most expensive calculations, while the HF/cc-pVTZ or cc-pVTQZ methods under-stabilize the 1C4 conformers [10]. The HF method supplemented with good quality basis sets tends to underestimate the H...OH interactions, because it overconcentrates the electron density around the atoms and in the normal covalent bonding regions and underconcentrates it in the other regions of space. The 1C4 conformations are sensitive to this effect because the strength of the 1-3 OH interactions may easily be decreased by small (low energy) deformations of the 1C4 ring and the exocyclic hydroxyl groups causing considerable increase in the H...O distances. The monotonic change in the relative stabilities as a function of basis set quality provides an opportunity to find a basis set for which the basis set truncation error compensates the inherent deficiencies of the HF method for the relative energies of the 4 conformers studied in this letter. Using a double-zeta quality basis set is close to the optimal choice for this type of energetic order at HF level of theory (c.f. Table 1).
The results of Barrows et al. [10] show that the inclusion of the electron correlation at MP2, CCSD/6-31G(d), and MP2/cc-pVDZ levels of theory provide rather poor energetic order (Table 1). This is expected because of the introduction of electron correlation increases the H...OH stabilization effects for the 1C4 ring relative to the HF method, thus necessarily worsen the good HF results by 6-7 kcal/mol. Considerably larger basis sets (cc-pVTZ or larger, c.f. Table 1) are required at MP2 level of theory to approach the real energetic order somewhat better. It should be noted that even this level of theory is not fully satisfactory and further basis set and correlation corrections are necessary to improve the results [10]. This behavior limits the applicability and value of MP2 calculations for conformational studies of aldo-hexapyranoses. It should be noted that the computational expense of the MP2 method is formally O(N5), where N is the number of basis functions in the molecule. The DFT methods may provide a less expensive alternative of estimating the correlation effects. The cost is formally O(N3), which may be reduced by efficient implementations [24].
The results in the Table 1 show that the various DFT methods supplemented with the double-zeta quality basis set provide similar energetic results as the MP2 method. They fail the same way as the MP2 method failed. However, the results also show that addition of the diffuse functions (e.g. 6-31+G(d) or aug-cc-pVDZ) improve considerably the DFT energetic order. This is because the diffuse functions provide a space for the electrons far from the nuclei, thus the long range part of the correlation and exchange functionals work better for the OH...O interactions. Similar behavior was experienced by Del Bene et al. [25] for the weak interactions with B3LYP functional. The inclusion of the exact exchange into the functional (B3P or B3LYP methods) improves the agreement between the DFT and MP2 or composite results (c.f. Table 1) considerably. Most of the energy calculations were performed with the MP2/cc-pVDZ geometries, because the geometry optimizations are rather expensive. The energetic effect of the geometry optimization was studied for the BP/6-31+G(d) and the B3LYP/6-31+G(d) calculations. The agreement with the best composite energy is slightly improved in the former and slightly worsened in the latter case by the geometry optimization. The relative energy changes are below 1.5 kcal/mol (c.f. Table 1)
The reproduction of the correct energetic order for the two 4C1 hydroxymethyl rotamers (1 and 2) is also a challenging task for the various methods. According to the experimental results the T rotamer is less stable than the G+ rotamer. The HF and MP2 methods are able to reproduce this energetic order only with the largest basis sets (c.f. Table 1). The HF, MP2 or CCSD methods supplemented with polarized double-zeta quality basis sets provide the opposite energetic order than the experiment by 0.15-0.50 kcal/mol.(c.f. Table 1). Our recent GGA-DFT/6-31G(d) calculations provided even larger (0.7-0.8 kcal/mol) relative stabilization for the T rotamer compared to the G+ rotamer [12]. Only the B3P/aug-cc-PVDZ//MP2/cc-pVDZ calculations indicated the G+ rotamer (1) to be slightly more stable than the T rotamer (2).
3.2. Molecular geometry
For G-g+ hydroxymethyl rotamer of 4C1 beta-D-glucose, (1), the experimental X-ray crystal structure is available [26]. The MP2/cc-pVDZ calculated geometry is in a good agreement with the experimental results for the bond lengths [10]. The largest deviation is 0.01 A (c.f. Table 2). The endocyclic torsional angle differences between the calculated and experimental geometry range up to 5o, these variations however, can be attributed to crystal packing effects [27]. Experimental data are not available for the other three conformers. For these conformers we take the MP2/cc-pVDZ calculated geometries as a reference.
A small structural
database for the optimized geometries is available from the authors. This page can be
conveniently viewed if MDL
Chemscape plug-in is installed. The results in the Table 2 show
that the bond lengthening correlation effects are largest in the BP/6-31G(d) method.
Adding diffuse functions to the heavy atoms provide a very small further bond lengthening
(about 0.002 A). The BP method clearly overcorrelates compared to the MP2 method in this
sense. The introduction of the exact exchange in the hybrid forms of B3P or B3LYP
decreases the bond lengthening effects. The results in Table 2 suggest the following
relations for the C-C, and C-O bond lengths: r(HF) < r(B3P) < r(MP2) < r(B3LYP)
< r(BP) (all methods are supplemented with 6-31G(d) or 6-31+G(d) basis sets). This
observation is in a perfect agreement with our earlier observations for C-O and O-H bond
lengths with double and triple-zeta quality basis sets [28].
The difference between the B3P, MP2 and B3LYP results is small (c.f. Table 2). It should
be noted that for the bond angles the BP method shows a better agreement with the MP2
results than the hybrid methods (c.f. Table 2). The grid size influences the calculated
molecular geometries only marginally (c.f. Tables 2 and 3). This makes it possible to use
the more economical sg1 grid instead of the more expensive fine grid for sugar
calculations.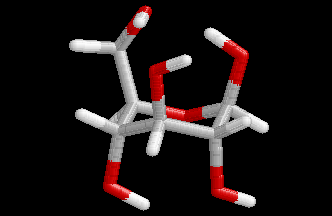
The B3LYP/6-31+G(d) calculations
differ considerably from the MP2 and other calculations for 1C4
conformer (4). The MP2 results show that the hexapyranose ring in this conformer is
distorted by the O5...H2-O2...H4 and O1...H3-O3...H6-O6...H1 interactions. In the
B3LYP/6-31+G(d) equilibrium geometry the C3-C2-O-H and C4-C3-O-H dihedral angles rotate from their starting positions
(g++ and g--, respectively) toward t positions, resulting considerably
smaller ring distortion and breaking the O1...H3 and O5...H2 interactions. Similar results
were obtained by HF/6-31G(d)
and BP/6-31+G(d)
calculations for the C3-C2-O-H dihedral angle (Table 3).
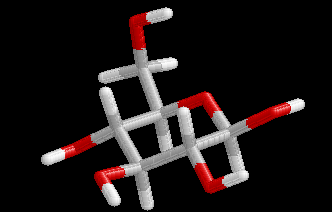
These differences are visualized in the Figures 2 and 3.
|
|
| Figure 2. Comparison of the B3LYP/6-31+G(d) structure (pink) with the MP2/cc-pVDZ structure (hydrogen atoms: white, carbon atoms: gray, oxygen atoms red) for conformer (4). Note that the geometry optimization was started from the MP2 structure. | Figure 3. Comparison of the BP/6-31+G(d) structure (pink) with the MP2/cc-pVDZ structure (hydrogen atoms: white, carbon atoms: gray, oxygen atoms red) for conformer (4). Note that the geometry optimization was started from the MP2 structure.. |
Table 3 shows the method and conformer dependence of the main geometric components of the O...H interactions. The difference between the ideal and calculated C-C-OH dihedral angles may signal the strength of the interaction. For the 4C1 conformers the HF method turns these dihedral angles toward their ideal values, while the inclusion of the electron correlation provides larger difference from the ideal values (c.f. Table 3 ). For 1C4 conformers, (3) and (4), the deviations of the C-C-O-H dihedral angles are as large as 40o and 55o, respectively. In these conformers the repulsive eclipsing interactions of the OH groups with the ring C-C bonds is counterbalanced by the O...H interactions and nearly eclipsed rotamers occur. However, this effect is rather sensitive to the method and basis set. For the conformer (4) the inclusion of the diffuse functions into the basis set turns away the second and third OH groups from the O4 and O1 atoms (c.f. B3LYP or BP method in Table 3 and figs 2 and 3), respectively. This not only decreases the repulsive eclipsing interactions, but it also decreases the distortion of the ring as it was noted above. It is probable that larger basis sets would influence the MP2 results of Barrows et al. [10], too. Conformer (3) shows a fair stability in this respect. It should be noted that the H-C(n)-O-H dihedral angles, measurable by NMR experiments, can be derived within 3o error bar from the C(n+1)-C(n)-O-H dihedral angles by subtracting 120o (if n = 1, 3) or adding 120o (if n = 2, 4) to them at HF and GGA-DFT levels of theory [12].
Some of the earlier characterization of the O...H interactions used the O...H distance and one angle (e.g. O...H-O or R-O-C...H out of plane angle [29]). The O...H-O angle is not discussed here, because the linearity and non-linearity of the O...H-O angle is extensively discussed in the literature [30] and this parameter is completely insensitive to spatial arrangement of the oxygen lone pairs. Also in sugars this angle is determined by other geometrical constrains and it deviates considerably from 180. The low experimental IR frequencies for the proton acceptor bending signal that the energy hypersurface is flat in this direction and little energy is required to reorient the acceptor molecule [30]. The O...O distance and two angles are used for the precise description of symmetric, Cs water dimer [31] or methanol and sylanol dimers [32].
Alternatively the O...H interactions for non symmetric cases can be characterized in a polar coordinate system centered on the O atom by three coordinates that provide the exact position of the H atom: the O...H distance, the C-O...H angle and the R-O-C...H dihedral angle.
Bader et al. has shown that two minima exist for the Laplace concentrations of electron density around the O atoms [33]. These minima are rigorous and exact mathematical representations of the O lone-pairs. The position of these minima can be characterized the same way as the position of the H atoms (the sign of the dihedral angle tells at which side of the molecule the points are). The angular position of the points where negative Laplacian attains its minimal value are (LM) are 99-100o and 104-105o for the C-O-LM and R-O-C...LM angles, respectively. Marshall et al. [34]considered these points as a site of electrophilic attack by the H atoms. The analysis of the 3D isosurfaces of the norm of the electron density gradient shows that an elliptic lens shaped surface appear around the bond critical point between the interacting O an H [35]. The analysis of the 3D isosurfaces of the negative Laplacian concentration around the minima shows that the negative Laplacian concentration remains considerably large between the two minima (large torsion angles) and a sharp cut off experienced at small angles (below 90o). Our investigation of the O...H interactions in the 1,2-ethanediol also show that the interaction is spatially extended []. The detailed discussion of the shape of the Laplacian concentration are out of the scope of the present letter and it will be given in a subsequent paper.
The results in Table 3 show that the various O...H interactions can readily be differentiated by the proposed geometric parameters. In the 4C1 conformers the O...H distances, the C-O...H bond angles and the R-O-C...H torsion angles are in the range of 2.26-2.45 A, 77-80o and 140-150o, respectively. The geometric parameters of the O4...H6 interaction in conformer (2) are different from these values (Table 3). For 1C4 conformers the O...H distances are considerably smaller (1.72-1.95 A) signaling a stronger interaction. The only exception is the O5...H2 interaction in conformer (4). For 1C4 conformers the C-O...H angles are closer to their optimal values and this gives a considerable stability for conformer (3), in which the dihedral angles are also close to their optimal values. In conformer (4) the O1...H3 and O5...H2 interactions are particularly weak. This can be attributed to the small C-O...H and/or R-O-C...H angles. The small angles for C-O...H or R-O-C...H provide weaker interaction while large R-O-C...H torsion angles (above 120o) are not so disadvantageous. This supports our proposition that the shape of the negative Laplacian concentration around the O atom plays a role in the interaction.
5. Conclusions
The following conclusions can be drawn from the discussion above:
Acknowledgment. The authors are grateful to Alfred D. French for the MP2/cc-pDVZ coordinates and for a preprint of Ref. 10. The financial support of the Hungarian Research Foundation (OTKA T14975, and T16328) is acknowledged. The continuos financial support of the Natural Sciences and Engineering Research Council (NSERC) is gratefully acknowledged.
[1] J. W. Brady, J. Am. Chem. Soc. 111 (1989) 5155.
[2] B. P. Van Eijck, Kroon-Batenburg, L. M. J.; Kroon, J. Mol. Struct. 237 (1990) 315.
[3] S. Ha, J. Gao, B. Tidor, J. W. Brady and M. Karplus, J. Am. Chem. Soc.113, (1991) 553.
[4] P. L. Polavarapu, C. S. Ewig, J. Comput. Chem. 13 (1992) 1255.
[5] R. G. Zhbankov, J. Mol. Struct. 275 (1992) 645.
[6] C. J. Cramer and D. G. Truhlar, J. Am. Chem. Soc., 115 (1993) 5745.
[7] B. P. van Eijeck, R. W. W. Hooft and J. Kroon, J. Phys. Chem., 97 (1993) 12093.
[8] U. Salzner and P. v. R. Schleyer, J. Org. Chem. 59 (1994) 2138.
[9] T. M. Glennon, Y. J. Zheng, S. M. Legrand, B. A. Shutzberg, and K. M. Merz Jr, J. Comp. Chem., 15 (1994) 1019.
[10] S. E. Barrows, F. J. Dulles, C. J. Cramer, A. D. French, and D. G. Truhlar, Carbohydr. Res., 276 (1995) 219.
[11] M. K. Dowd, A. D. French, and P. J. Reilley, Carbohydr. Res., 264 (1994) 1.
[12] G. I. Csonka, I. Kolossváry, P. Császár, K. Éliás, and I. G. Csizmadia, J. Mol. Struct. accepted.
[13] Y. Nishida, H. Ohrui, H. Meguro, Tetrahedron Lett. 25 (l984) 1575.
[14] G. M. Brown and H. A. Levy, Acta Crystallogr. Sect. B (1979) 656.
[15] A.D. Becke, Phys. Rev. A, 38 (1988) 3098.
[16] J.P. Perdew, Phys. Rev. B, 33 (1986) 8822.
[17] S. H. Vosko, L. Wilk and M. Nussair, Can. J. Phys., 58 (1980) 1200.
[18] A.D. Becke, J. Chem. Phys., 98 (1993) 5648.
[19] M. J. Frisch, G. W. Trucks, M. Head-Gordon, P. M. W. Gill, M. W. Wong, J. B. Foresman, B. G. Johnson, H. B. Schlegel, M. A. Robb, E. S. Replogle, R. Gomperts, J. L. Andres, K. Raghavachari, J. S. Binkley, C. Gonzalez, R. L. Martin, D. J. Fox, D. J. DeFrees, J. Baker, J. J. P. Stewart, and J. A. Pople, Gaussian 92/DFT, Revision G, Gaussian, Inc., Pittsburgh PA, 1993.
[20] C. Lee, W Yang and R. G. Parr, Phys. Rev. B 37 (1988) 785.
[21] M. J. Frisch, G. W. Trucks, M. Head-Gordon, P. M. W. Gill, M. W. Wong, J. B. Foresman, B. G. Johnson, H. B. Schlegel, M. A. Robb, E. S. Replogle, R. Gomperts, J. L. Andres, K. Raghavachari, J. S. Binkley, C. Gonzalez, R. L. Martin, D. J. Fox, D. J. DeFrees, J. Baker, J. J. P. Stewart, and J. A. Pople, Gaussian 94, Revision B, Gaussian, Inc., Pittsburgh PA, 1995.
[22] W. J. Hehre, L. Radom, P.v. R. Schleyer and J. A. Pople, Ab Initio Molecular Orbital Theory, John Wiley & Sons, New York, 1986, and references cited therein.
[23] T. H. Dunning, J. Chem. Phys., 90 (1989) 1007.
[24] P. M. W. Gill, B. G. Johnson, J. A. Pople, Chem. Phys. Lett. 217 (1994) 65.
[25] J. E. Del Bene, W. B. Person, K. Szczepaniak, J. Chem. Phys., 99 (1995) 10705.
[26] S.S.C. Chu and G.A. Jeffrey, Acta Crystallogr., B24 (1968) 830.
[27] A.D. French, R.S. Rowland and N.L. Allinger, in A.D. French and J.W. Brady (Eds.), Computer Modeling of Carbohydrate Molecules, ACS Symposium Series 430, American Chemical Society, Washington DC, 1990 p 120.
[28] G. I. Csonka, I. G. Csizmadia, Chem. Phys. Lett. 243 (1995) 419.
[29] L. Van den Enden, C. Van Alsenoy, J. N. Scarsdale,, L. Shäfer, J. Mol. Struct. (Theochem), 104 (1983) 471.
[30] S. Sheiner, in K.B. Lipkowitz and D.B. Boyd (Eds.),Rewievs in Computational Chemistry, Vol II, VCH, New York, 1991, p 165, and references cited therein.
[31] M. J. Frisch, J. E. Del Bene, J. S. Binkley and H. F. Schaefer III, J. Chem. Phys., 84 (1986) 2279.
[32] A. Bleiber and J. Sauer, Chem. Phys. Lett., 238 (1995) 243.
[33] R. F. W. Bader, P. J. MacDougall, C. D. H. Lau, J. Am. Chem. Soc. 106 (1984) 1594.
[34] M. T. Carrol, C. Ghang, and R. F. W. Bader, Mol. Phys. 63 (1988) 387.
[35] G. I. Csonka, N. Anh, J. Ángyán, and I. G. Csizmadia, Chem. Phys. Lett. 245 (1995) 129.
