Edifices ioniques
Il existe trois types de réseaux ioniques hétérodinucléaires (de type AB) :
Généralités
L'expérience montre que les différents solides ioniques de type AB se répartissent selon les trois grandes classes de mailles que sont :
- la maille cubique centrée (CC),
- la maille cubique à face centrée (CFC) et
- la maille blende ou la maille wurtzite,
classé simplement selon x, définit comme le rapport du rayon du cation sur le rayon de l'anion :
x = r+ / r-
Les résultats expérimentaux montrent que l'on a un réseau de type :
CsCl si 0,73 < x < 1 NaCl si 0,41 < x < 0,73 ZnS si 0,23 < x < 0,41 De considérations assez simples permettent de retrouver ces résultats.
Maille cubique centrée (CC) de type chlorure de césium CsCl
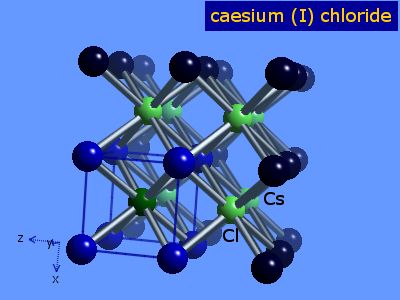
On choisit de représenter la maille cubique centrée avec l'ion césium au centre de la maille et les ions chlorures aux sommets de la maille. Le paramètre de maille, c'est-à-dire la distance entre les deux ions chlorures est noté a.
Stoechiométrie de la maille
- Dans cette maille, la contribution de l'ion césium est de 1 et la contribution des 8 ions chlrorures et 1/8 : 8 . 1/8 = 1.
- On retombe bien sur une stoechiométrie 1 : 1.
Indices de coordination
Chaque ion césium est entouré de 8 ions chlorure, et chaque chlorure de 8 ions césium. Il s'agit d'une coordination cubique 8-8.
Calcul de l'intervalle de x
Le rayon minimum du cation r+ min correspond à la situation où les ions césium et chlorure sont tangents. On calcule r+ min sur la diagonale du cube :
a Ö3 = 2 r- + 2 r+ min
Or les ions chlorures sont tangents sur l'arête de la maille :
a = 2 r-
Donc : 2 r- Ö3 = 2 r- + 2 r+ min
Soit : r+ min = r- (Ö3 - 1 )
Soit : xmin = r+ min/ r-= Ö3 - 1 = 0,732
Le rayon maximum du cation r+ max est choisi pour : r+ = r-
Soit : xmax = 1On en conclut qu'un solide ionique présente une maille cubique centrée de type CsCl si 0,73 < x < 1.
Exemples de structures CC de type CsCl
Solide CsCl CsBr CsI TlCl TlBr TlI a / pm 617 644 684 575 596 630 x 0,93 0,87 0,78 0,83 0,77 0,67 Les cristaux qui font exception à la régle précédemment énoncée sont indiqués en italique.
Maille cubique à face centrée (CFC) de type chlorure de sodium NaCl
On choisit de représenter la maille cubique faces centrées avec les ions chlorures aux sommets de la maille et les ions sodium entre chaque paire d'ions chlorure. Le paramètre de maille, c'est-à-dire la distance entre les deux ions chlorures est noté a.
Stoechiométrie de la maille
- Dans cette maille, il y a 12 ions sodium (ceux de arêtes) apportant une contribution 1/4 à la maille et 1 ion sodium (celui du centre) apportant une contribution de 1 : 12 . 1/4 + 1 = 4.
- Il y a 8 ions chlrorures (ceux des sommets) qui contribuent pour 1/8 dans la maille et 6 ions chlorures (ceux des faces) qui contribuent pou 1/2 : 8 . 1/8 + 6 . 1 / 2 = 4
- On retombe bien sur une stoechiométrie 1 : 1.
Indices de coordination
Chaque ion sodium est entouré de 6 ions chlorure, et chaque chlorure de 6 ions sodium. Il s'agit d'une coordination octaédrique 6-6.
Calcul de l'intervalle de x
Le rayon minimum du cation r+ min correspond à la situation où les ions sodium et chlorure sont tangents. On calcule r+ min sur une arête :
a = 2 r- + 2 r+ minOr les ions chlorures sont tangents sur la diagonale d'une face :
a Ö2 = 4 r-
Par conséquent : 2 r- + 2 r+ min = 4 r- / Ö2
Soit : r+ min = r- ( 2 / Ö2 - 1) : r+ min = r- ( Ö2 - 1)
Soit : xmin = r+ min/ r-= Ö2 - 1 = 0,414Le rayon maximum du cation r+ max est celui imposé par la contrainte précédente qui impose pour une structure de type CC (CsCl) une valeur minimale de x de 0,732.
On en conclut qu'un solide ionique présente une maille cubique faces centrées de type NaCl si 0,41 < x < 0,73.
Exemples de structures CFC de type NaCl
Solide LiF NaF NaCl NaBr NaI KCl a / pm 402 464 564 598 647 629 x 0,44 0,70 0,52 0,49 0,44 0,73 Solide KBr KI RbCl RbBr RbI a / pm 660 707 658 689 734 x 0,68 0,62 0,82 0,76 0,69 Les cristaux qui font exception à la régle précédemment énoncée sont indiqués en italique.
Exemples de structures CFC de type NaCl Arséniures Carbures Bromures Chlorures Fluorures Hydrures Iodures SnAs TiC LiBr LiCl LiF LiH LiI UC NaBr NaCl NaF NaH NaI KBr KCl KF KI AgBr RbCl RbF RbI AgCl AgF
Nitrures Oxydes Oxydes Sélénures Sulfures Télurures LaN MnO MgO MgSe MgS CaTe ScN FeO CaO CaSe CaS SrTe TiN CoO SrO SrSe SrS BaTe UN NiO BaO BaSe MnS CdO TiO
Maille blende de type ZnS-blende
On choisit de représenter la de type blende avec les ions chlorures aux sommets de la maille et les ions zinc au coeur de la maille. Le paramètre de maille, c'est-à-dire la distance entre les deux ions chlorures est noté a.
Stoechiométrie de la maille
- Dans cette maille, il y a 4 ions zinc (au ceour de la maille) apportant chacun une contribution de 1 à la maille : 4. 1 = 4.
- Il y a 8 ions chlrorures (ceux des sommets) qui contribuent pour 1/8 dans la maille et 6 ions chlorures (ceux des faces) qui contribuent pou 1/2 : 8 . 1/8 + 6 . 1 / 2 = 4
- On retombe bien sur une stoechiométrie 1 : 1.
Indices de coordination
Chaque ion zinc est entouré de 4 ions chlorure, et chaque chlorure de 4 ions zinc. Il s'agit d'une coordination tétraédrique 4-4.
Calcul de l'intervalle de x
Le rayon minimum du cation r+ min correspond à la situation où les ions zinc et chlorure sont tangents. On calcule r+ min sur le quanrt de la diagonale du cube : 1 / 4 . a Ö3 = r- + r+ min
Or les ions chlorures sont tangents sur la diagonale d'une face :
a Ö2 = 4 r-
Soit : a = 4 r- / Ö2
Par conséquent : r+ min = 1 / 4 . a Ö3 - r-: r+ min = r- (Ö3 / Ö2 - 1)
Soit : r+ min = r- (Ö1,5 - 1)
Soit : xmin = r+ / r-= Ö1,5 - 1 = 0,225Le rayon maximum du cation r+ max est celui imposé par la contrainte précédente qui impose pour une structure de type CFC (NaCl) une valeur minimale de x de 0,414.
On en conclut qu'un solide ionique présente une maille cubique faces centrées de type ZnS si 0,225 < x < 0,41.
| Exemples de structures blende de type ZnS | |||||
| Sulfures | Tellurures | Sélénures | Hydrures | Oxydes | |
| BeS | BeTe | BeSe | TiH | ZnO | |
| MnS | ZnTe | MnSe | ZrH | ||
| ZnS | CdTe | ZnSe | |||
| CdS | HgTe | HgSe | |||
| HgS | |||||
| Chlorures | Bromures | Iodures | Carbures | Arséniures | Phosphure |
| CuCl | CuBr | CuI | SiC | AlAs | AlP |
| AgI | |||||
Maille würtzite de type ZnS-würtzite
Le traitement est le même que pour la maille de type blende.