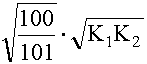- Először oldjuk meg a feladatot a szokásos módon.
HA A- H+ K: 1 0 R: - 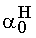
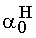
E: 1- 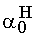

1,8 ·10-5 Mivel csak a molarányokat akarjuk számítani és az abszolút koncentrációk érdektelenek, vehetjük a kezdeti savkoncentrációt egységnyinek. Az egyensúlyi hidrogénion-koncentráció 1,8·10-5 M.
Kc =
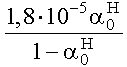 = 1,8·10-4, ahonnan
= 1,8·10-4, ahonnan 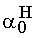 = 0,909 és
= 0,909 és 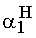 = 0,091.
= 0,091. - A (XI. 1) egyenletbe behelyettesítve az
eredményt azonnal kapjuk:
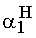 =
= 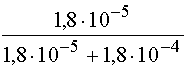 =0,091
=0,091 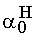 = 1-
= 1-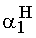 = 0,909
= 0,909
Azaz, míg ugyanezen a pH értéken (pH = 4,74) az ecetsav disszociációja 50%-os, addig a nem jelentősen erősebb hangyasavé már 90,9%-os.
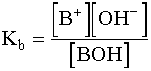
cb = [BOH]T = [BOH] + [B+]
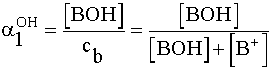 =
= 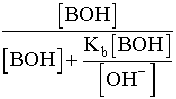 =
= 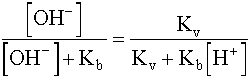
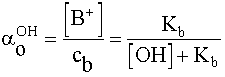
- Az előző példához hasonlóan a kezdeti savkoncentrációt
egységnyinek választva, valamint az egyensúlyi [H+] koncentrációt 10-7-nek
véve a két konszekutív egyensúlyra a következő mérlegeket írhatjuk fel:
H2SO3 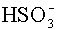
H+ K: 1 0 R: -x x E: 1-x x 10-7 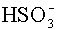
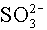
H+ K: x 0 R: -y y E: x-y y 10-7 Az egyes komponensek egyensúlyi koncentrációi: [H2SO3] = 1-x; [
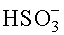 ] = x-y; [
] = x-y; [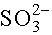 ] = y, [H+]
= 10-7. Behelyettesítve a tömeghatástörtekbe:
] = y, [H+]
= 10-7. Behelyettesítve a tömeghatástörtekbe: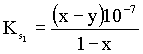 ,
, 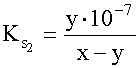
Ebből:
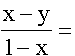 1,7.105 ill.
1,7.105 ill. 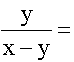 0,63
0,63Melyből megoldva az egyenleteket, kapjuk:
1 - x =
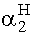 = 6,41· 10-6
= 6,41· 10-6
x - y =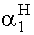 = 0,641
= 0,641
y =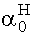 = 0,359
= 0,359
- Oldjuk meg a feladatokat a (XI. 3)-(XI. 5) kifejezések
segítségével!
Először a (XI. 3)-(XI. 5) kifejezések közös nevezőjét számítjuk ki; jelöljük ezt a’-vel.
a’ = [H+]2 + K1 [H+] + K1K2 = 10-14 + 1,7· 10-2· 10-7 + 1,7· 10-2· 6,3· 10-8 =
= 10-14 + 1,7· 10-9 + 9,52· 10-10 = 2,652· 10-9
Ezután az egyes molarányok:
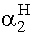 =
= 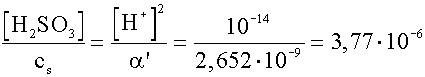 ®
3,77· 10-4%
®
3,77· 10-4%
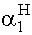 =
= 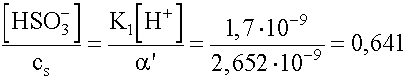 ®
64,1%
®
64,1%
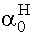 =
= 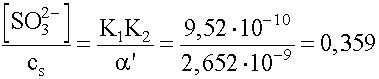 ®
35,9%
®
35,9%
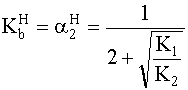 = 0,120
= 0,120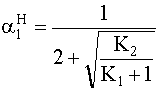 = 0,760
= 0,760[H2SO4] = 0;
A Brönsted-Charlot egyenletbe
helyettesítve kapjuk: 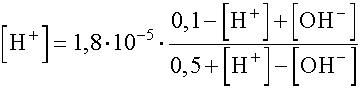
Mivel az ecetsav csak kismértékben disszociál és kémhatása savas lesz,
feltételezhetjük, hogy [H+] « 0,1, ill. [H+] » [OH-].
Így: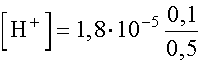 ,
,
vagy általában 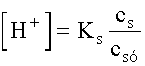 ,
a IX. fejezetből ismert Henderson-egyenletet.
,
a IX. fejezetből ismert Henderson-egyenletet.
Innen ![]() = 3,6·10-6
® pH = 5,44
= 3,6·10-6
® pH = 5,44
- Használjuk a Henderson egyenletet:
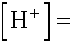
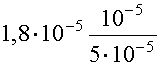 = 3,6·10-6
® pH = 5,44
= 3,6·10-6
® pH = 5,44
Az eredmény megegyezik az előző példáéval.Tanulmányozva azonban a Brönsted-Charlot egyenletet, könnyen észlelhetjük, hogy most a
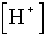 nem
hanyagolható el cs, ill. csó mellett, eredményünk tehát
félrevezető.
nem
hanyagolható el cs, ill. csó mellett, eredményünk tehát
félrevezető. - Mivel most csak a [H+] >>
 teljesül, így a
teljesül, így a 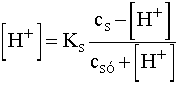 =
= 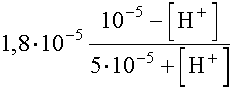
kifejezést kell használnunk.
A másodfokú egyenlet megoldásával kapjuk:
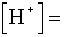 2,55·10-6 ®
pH = 5,59
2,55·10-6 ®
pH = 5,59
Az eredményből látszik, hogy a Henderson egyenlet használata nem ad kielégítően pontos eredményt, ill. hogy az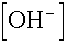 majdnem három nagyságrenddel kisebb a
majdnem három nagyságrenddel kisebb a 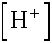 -nál, így
elhanyagolásunk jogos volt.
-nál, így
elhanyagolásunk jogos volt.
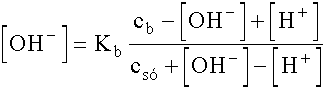
Mivel a várható kémhatás bázikus lesz ([OH]- » [H+]), ezért a törtben a [H+] elhanyagolásával keressük először a megoldást.
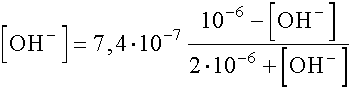
rendezve: [OH-]2 + 2,48· 10-6 [OH-] - 7,4· 10-13 = 0
innen: [OH-] = 2,69· 10-6 ® pOH = 6,57 ® pH = 7,43
Eredményünk szerint a [H+] az [OH-] értékének mintegy hatoda, ezért érdemes az eredeti egyenlet megoldásával pontosabbá tenni eredményünket.
azaz 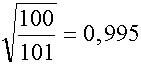 , tehát a hiba 5
ezrelék, így minden gyakorlatilag fontos esetben közelítésünk megengedett.
, tehát a hiba 5
ezrelék, így minden gyakorlatilag fontos esetben közelítésünk megengedett.
a = 1 + 1,4·104· 10-3
+ 4· 10-2· 103 + 3· 1010 · 10-9 +
3,3· 1012· 10-12
a = 1 + 14 + 40 + 30 + 3,3 = 88,3
(XI. 17) szerinti moltörtek:
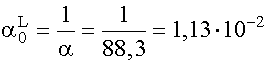 ;
;
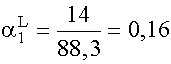 ;
; 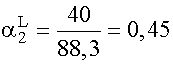 ;
;
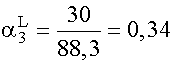 ;
; 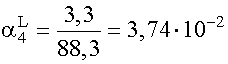
A molkoncentrációk (XI. 15) szerint:
[M] = ![]() = 1,13· 10-2· 10-1
= 1,13· 10-3 M
= 1,13· 10-2· 10-1
= 1,13· 10-3 M
[ML] = ![]() = 1,6· 10-1· 10-1
= 1,6· 10-2 M
= 1,6· 10-1· 10-1
= 1,6· 10-2 M
[ML2] = ![]() = 0,45· 10-1 = 4,5· 10-2 M
= 0,45· 10-1 = 4,5· 10-2 M
[ML3]= ![]() = 0,34· 10-1 = 3,4· 10-2 M
= 0,34· 10-1 = 3,4· 10-2 M
[ML4] = ![]() = 3,74· 10-2· 10-1 = 3,74· 10-3 M
= 3,74· 10-2· 10-1 = 3,74· 10-3 M
és a ligandum teljes koncentrációja (14) szerint:
cL = 10-3+ 1,6· 10-2+ 2· 4,5· 10-2+
3· 3,4· 10-2+4· 3,74· 10-3= 0,224 M
(XI. 18 ) alapján: a = 1 + 1,7· 109 · 10-4 + 3,2· 1012 · 10-8 = 1 + 1,7· 105 + 3,2· 104 =2,02· 105
(XI. 17) szerint:
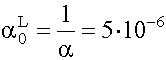
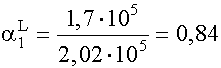
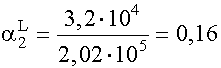
(XI. 13)-ból cM = [M] · a = 2,02· 103
(XI. 15) szerint a molkoncentrációk:
[M] = 10-2 M
[ML] =
[ML2] =
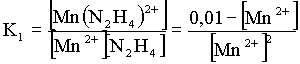 = 5,8· 104
= 5,8· 104mivel
A másodfokú egyenletet megoldva kapjuk:
Feltételezve, hogy a berillium teljes
mértékben a maximális koordinációs számú komplex, ![]() formában van jelen, az ehhez szükséges
fluorid mennyiség:
formában van jelen, az ehhez szükséges
fluorid mennyiség:
3 [Be2+]T = 5· 10-2
Ebből a becslés:
[F-] = [F-]T - 5· 10-2
= 8,33· 10-2 - 5·
10-2 = 3,33· 10-2
Ezután ellenőrizzük feltételezésünket. Számítsuk ki az egyes moltörteket. A
részletek mellőzésével kapjuk:
![]()
![]()
![]()
![]()
Az eredmény mutatja, hogy a feltételezés gyakorlatilag elfogadható. A Be2+
kevesebb, mint 3%-a van más formában, mint ![]() . Ezután a b 3
összefüggésből kapjuk:
. Ezután a b 3
összefüggésből kapjuk:
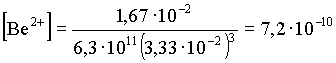
A korábban részletesen leírtak szerint a molkoncentrációk:
[M] = 7,2· 10-10 [ML] = 3· 10-6 [ML2] = 5·
10-4 [ML3] = 1,67· 10-2
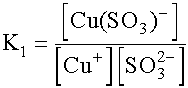
tehát c = [Cu(SO3)-]= 2· 10-2 és [Cu+]= [
[Cu+] =
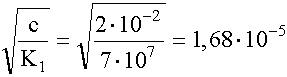
Ellenőrzésképpen kiszámítjuk a moltörteket:
Az eredmények igazolták feltételezésünket, mivel az 1:1 komplex az oldat 99,9%-át alkotja. A molkoncentrációk:
[M] = 1,6· 10-5 [ML] = 2· 10-2 [ML2] = 2,4· 10-6
[ML2] = 3,8 10-3 M [ML3] = 3,8· 10-3 M
[ML4] = 10-3 M [ML5] = 4 ·10-5 M
[ML] = 0,011 M
[ML2] = 0,039 M
[ML3] = 0,038 M
[ML4] = 0,011 M
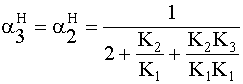 » 0,5
» 0,5 » 0
» 0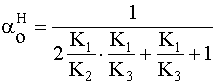 » 0
» 0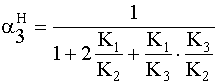 ~0,
~0, 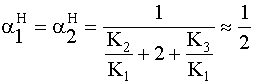
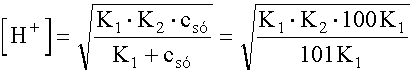 =
=