dynamique
La fonction entropie, S
Le deuxième principe de la thermodynamique
Il existe, pour toute transformation thermodynamique, évoluant d'un état initial I à un état final F, une fonction d'état extensive S appelée fonction entropie, la variation d'entropie DS du système:
DS = SFinal - SInitial
Pour une transformation finie, la variation d'entropie DS du système est la somme de deux termes :
DS = eS + iS
eS est l'entropie d'échange ou entropie de transfert : c'est la variation d'entropie due aux échanges de chaleur entre le système et le milieu extérieur.
iS est l'entropie interne ou entropie créée au sein du système.
eS et iS dépendent de la nature de la transformation (ne sont pas functions d'état).
Pour une variation élémentaire :
dS = deS + diS
dS est une différentielle exacte, deS et diS, ne le sont en général pas.
L'entropie de l'univers croît. L'entropie créée au sein du système est donc toujours positive ou nulle. Elle est nulle pour une transformation réversible (fictive). Elle est positive pour une transformation réelle, naturelle, c'est-à-dire irréversible.
- Pour une transformation finie réversible : iS = 0, pour une tranformation finie irréversible : iS > 0.
- Pour une transformation élémentaire réversible: diS = 0,
pour une transformation élémentaire irréversible : diS > 0.Relation entre entropie de transfert et quantité de chaleur échangée
Pout une transformation élémentaire, à T donné :
deS = dQ / T
Ce terme peut être positif ou négatif.
Calculs de variations d'entropie, DS
Cas d'une transformation monotherme pour un système fermé
Comme :
dS = diS + dQ / T
- Pour une transformation réversible : dS = dQ / T.
Pour une transformation irréversible : dS > dQ / T.
Cas d'un système isolé
Un système isolé n'échange ni matière ni chaleur avec le milieu extérieur, c'est-à-dire : dQ = 0, soit deS = dQ / T = 0. Comme dS = diS + dQ / T,
dS = diS
- Pour une transformation réversible : dS = 0.
- Pour une transformation irréversible : dS > 0.
Signification physique de l'entropie
L'entropie est une mesure du désordre : la création d'entropie correspond à l'accroissement du désordre microscopique du système.
On en déduit que si on passe d'un état ordonné à un état désordonné, l'entropie augmente, ce qui est le cas du passage de l'état solide à l'état liquide, et de l'état liquide à l'état gazeux.
De même, l'entropie d'un corps augmente donc lorsque l'agitation moléculaire augmente, c'est-à-dire lorsque la température s'élève (à pression constante).
Ces considérations sur le désordre microscopique ouvrent le champ de la thermodynamique statistique.
Avec plus de précision dans la définition, on dira que l'entropie mesure la dispersion "chaotique" de l'énergie. Les transformations spontanées tendent donc à minimiser cette dispersion en amenant les systèmes dans un état d'entropie maximale.
Entropie molaire d'un corps pur
Troisième principe de la thermodynamiqueEntropie molaire d'un corps pur
L'entropie molaire standard est définie par :
Sm(T, P) = S (T, P, n) / n
où Sm(T, P) est en J.K-1.mol-1.
On note Sm°(T) l'entropie molaire standard d'un corps pur à P = P° = 1 bar.
Principe de Nernst : 3ème principe de la thermodynamique
L'entropie molaire de tous les corps purs parfaitement cristallisés dans leur état stable est nulle à 0 K :
Sm(0 K, P, crist) = 0 et Sm°(0 K, crist) = 0
La signification de ce principe est qu'il n'y a aucun désordre dans un cristal pur à T = 0 K.
Remarques.
- Si le cristal présente des défauts (lacunes, interstitiels, dislocations...) : Sm°(0 K) > 0.
Si le cristal existe sous plusieurs formes allotropiques, Sm° = 0 pour la forme la plus stable.
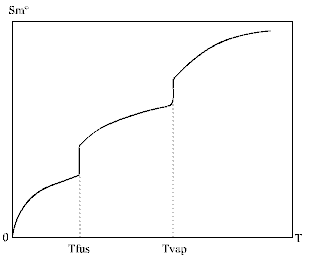
Les calculs seront effectués à pression constante.L'entropie molaire standard se calcule à partir de :
dSm°(T) = dQ / T
Or à P = Cte, on rencontre deux situations :
- soit : dQ = Cp°.dT
- soit : Q = DH°mchangement d'état
On en déduit que l'expression générale de calcul de Sm°(T) est :
Sm°(T) =
Sm°(0 K) +
DSm°( Cpm°(solide) dT / T , de T = 0 K à T(fusion) ) +
DH°(fusion) / T(fusion) +
DSm°( Cpm°(liquide) dT / T , de T = T(fusion) à T(vaporisation) ) +
DHm°(vaporisation) / T(vaporisation) +
DSm°( Cpm°(gaz) dT / T , de T(vaporisation) à T(final) )