dynamique
Fonction enthalpie
libre G
Fonction de Gibbs
La fonction enthalpie libre G est définie par l'expression :
G = H - TS
G est une fonction d'état extensive
La relation suivante est appelée relation de Gibbs-Helmholtz. Elle exprime la relation qui existe entre l'enthalpie libre et l'enthalpie interne.
¶
( G )P = - H ¶ T T T² Démonstration
Considérons une transformation élémentaire isotherme et isobare d'un système fermé dans lequel le travail se limite à celui des forces de pression. L'enthalpie libre est : G = H - TS On peut l'exprimer en fonction de l'énergie interne : G = U + PV - TS L'expression élémentaire de l'enthalpie libre est : dG = dU + P.dV + V.dP - T.dS - S.dT Avec : dU = dW + dQ Comme le système n'est sousmis qu'aux forces de pression : dW = -P.dV = -Pext.dV Or : dS = deS + diS = dQ / T + diS Soit : dQ = T.dS - T.diS L'expression de dG se simplifie : dG = V.dP - S.dT - T.diS G est fonction de P et de T : G = G(P, T). On peut exprimer dG en fonction de ses dérivées partielles : dG = (dG / dP)T dP + (dG / dT)P dT Par identification des deux dernières équations : V = (dG / dP)T S = - (dG / dT)P Comme : G = H - TS Alors : H = G + TS = G - T (dG / dT)P On peut diviser chaque membre par - T² : - H / T² = - G / T² + 1/T . (dG / dT)P En identifiant le second membre à la dérivée de G / T par rapport à T, à P constante on peut écrire :
Cette relation est appelée relation de Gibbs-Helmholtz
|
La condition d'évolution spontanée d'un système se traduit sur l'enthalpie libre par : dGT,P < 0 |
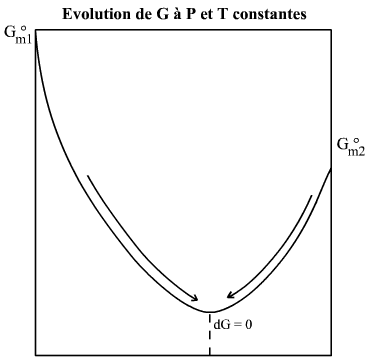
A pression et température contantes, un système va donc spontanément évoluer dans le sens de la diminution de G (dG < 0). Cette évolution cesse lorsque G est minimal, ce qui se traduit par dG = 0.
La condition d'équilibre d'un système est donc :
dGT,P = 0
Démonstration
Considérons une transformation
élémentaire isotherme et isobare d'un système fermé dans lequel le travail se limite
à celui des forces de pression. On peut l'exprimer en fonction de l'énergie interne : G = U + PV - TS L'expression élémentaire de l'enthalpie libre est : dG = dU + P.dV + V.dP - T.dS - S.dT Avec : dU = dW + dQ Comme le système n'est sousmis qu'aux forces de pression : dW = -P.dV = -Pext.dV Or : dS = deS + diS = dQ / T + diS Soit : dQ = T.dS - T.diS L'expression de dG se simplifie : dG = V.dP - S.dT - T.diS Pour une transformation isobare et isotherme : dG = - T.diS Dans le cas d'une réaction chimique (transformation naturelle donc irréversible) : diS > 0
dG = - T.diS < 0 |