összefüggés adja, melyben c a hullám
terjedési sebessége, azaz elektromágneses hullám esetén c a fénysebesség, értéke
3·108 m/s. Gyakran használják a hullámszám (n
*) fogalmát, mely a hullámhossz reciproka.A hullámmozgás sajátsága a hullámhossz (l
), amely a periodikus mozgás egy periódusának hosszát jelenti, valamint a frekvencia
vagy rezgésszám (n ), amely az időegység alatti periódusok
száma. A két mennyiség közötti kapcsolatot a összefüggés adja, melyben c a hullám
terjedési sebessége, azaz elektromágneses hullám esetén c a fénysebesség, értéke
3·108 m/s. Gyakran használják a hullámszám (n
*) fogalmát, mely a hullámhossz reciproka.
A fény elektromos jelenség, az atomok vonalas színképe, a karakterisztikus röntgensugárzás és számos más kísérleti tény bizonyítja, hogy a fény diszkrét adagokban terjed. 1-1 ilyen adag, kvantum, hordozója a foton. A foton energiáját az E = hn képlet adja meg, ahol h (= 6,6262·1034 Js) a Planck állandó.
Interferencia kísérletekkel kimutatható, hogy mikrorészecskék
hullámsajátsággal is rendelkeznek. Attól függően tehát, hogy az anyag milyen
kölcsönhatásait vizsgáljuk, hullám vagy részecske sajátságokat tapasztalunk.
Helytelenül ezt szokták a fény, ill. a részecskék "kettős" természetének
nevezni. Valójában az anyag nem "kettős" tulajdonságú, a kettősség
csupán képzeletünk, szemléletünk korlátaiból adódik. A n
hullámhosszú részecske impulzusát a 
összefüggés adja meg.
Mikrorendszerek leírására a Schrödinger egyenlet, egy másodrendű parciális differenciálegyenlet alkalmas. Ezt az egyenletet azonban zárt alakban csak hidrogénszerű atomokra lehet megoldani. A megoldásokból származó következtetéseket azonban – első közelítésben – más atomokra is alkalmazhatjuk.
Az alábbi táblázatban a hidrogénszerű atomok Schrödinger egyenletének megoldásaként kapott Y függvényeket tüntettük fel. Y indexei a fő- (n), mellék- (l) és mágneses (m) kvantumszámok, Z a magtöltés, ao (52,92 pm, az ún. Bohr-féle atomrádiusz, r, n , j a függvények három változója az origótól (mag középpont) mért távolság, a dőlésszög, ill. a csapásszög. A függvények alakjából jól látható, hogy mindegyikük szeparálható egy távolságfüggő (radiális) és egy szögfüggő (anguláris) részre:
Y (r, n , j ) = R(r)·Y(n ,j )
Hidrogénszerű atomok hullámfüggvényei |
|
|---|---|
| 1 s | Y 100 = |
| 2 s | Y 200 = |
| 2 p | Y 210 = |
Y 21-1 = |
|
Y 211 = |
|
| 3 s | Y 300 =  |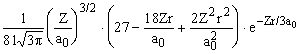
| 3 p | Y 310 =  |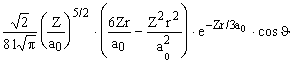
Y 31-1 =  |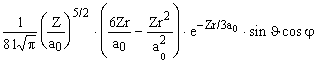
|
Y 311 =  |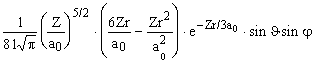
|
| 3 d | Y 320 =  |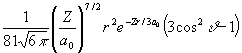
Y 32-1 =  |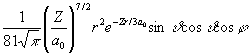
|
Y 321 =  |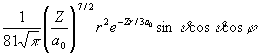
|
Y 32-2 =  |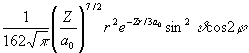
|
Y 322 =  |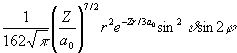
A következő táblázatban találhatunk részletes információt és 2, valamint 3 dimenziós ábrákat
Ha az elektronsűrűség eloszlására vagyunk kíváncsiak, M. Born szerint a Y2 függvényt kell vizsgálnunk, melynek értéke a tér minden pontjában arányos az elektron tartózkodási valószínűségével az illető pontban. Y2 megadja, hogy az origótól r távolságra egy infinitézimális dxdydz térfogatelemben mekkora az elektronsűrűség. Hogy válaszolni tudjunk arra a kérdésre, mekkora az elektron tartózkodási valószínűsége az origótól valamilyen r' távolságban egy dr vastagságú gömbhéjban, az adott távolságban levő gömbhéj térfogatával, 4p r2 dr-el kell szorozni a Y2 r-beli értékét. Így kapjuk meg a következő árán látható radiális eloszlást:
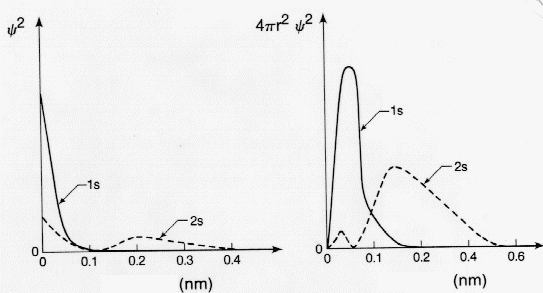
Természetesen, ha a Y függvény szögfüggő részt is tartalmaz, kétdimenziós koordináta-rendszerben nem tudjuk ábrázolni. Minthogy a Y függvény három változós, a függvényértékét csak egy negyedik koordinátán lehetne feltüntetni. Ezért leggyakrabban úgy járnak el, hogy a függvény értékét nem jelzik, csak az előjelét. (Néha sűrűsödő-ritkuló pontozással vagy egyéb módon szokták jelezni.) A függvények határait úgy jelzik, hogy a kialakuló térbeli alakon belül az elektron megtalálási valószínűsége 90% legyen. Ezt a térbeli alakot nevezik pályáknak. A pályák térbeli megjelenítésére nagyon akalmas a VRML (virtuális valóság modellezési nyelv).
Látható, hogy a függvények alakjából zérushelyek, ún. csomófelületek következnek. A csomófelületek számának és típusának megadásához egy egyszerű szabályt is adhatunk:
| összes csomófelület száma: | n-1 |
| csomógömbök száma: | n-l-1 |
| csomókúpok száma: | l-|m| |
| függőleges csomósíkok száma: | |m| |
A fenti szabályok alkalmazása csak akkor vezet azonban eredményre, ha ugyanekkor tudjuk és szem előtt tartjuk, hogy a csomófelületek egyben a függvények zérushelyei.
Meg kell jegyezni, hogy az atompálya definíciója nem azonos az atom méretének definíciójával. Az atom méretének csupán egyik meghatározója az elektronok eloszlása. Ha eltekintünk attól, hogy az r növekedtével az elektron megtalálási valószínűsége sohasem válik zérussá, és így a pálya kihasítása mindig önkényes, még akkor is függ az atom nagysága a környező atomoktól. Ezért az atom "mérete" feltételről feltételre, kötésről kötésre változik. Mindamellett gyakran használják az atom-, ill. ionrádiusz adatokat jelenségek összehasonlításához és jellemzéséhez.
A kvantumszámoknak geometriai jelentésükön kívül sokkal mélyebb értelmük is van. A Schrödinger-egyenlet megoldásakor a Y "sajátfüggvényeken" kívül az energia sajátértékeket, azaz a pályák energiaértékeit is megkapjuk. Ezek az értékek hidrogénszerű atomokra csak az n, egyébként n és l értékeitől függenek. Pl. H atomra:
(eV)
(ahol m az elektron tömege, e a töltése).
Hasonlóképpen határozza meg l a pálya impulzus- és mágneses momentumát:
illetve m az impulzus-, ill. mágneses momentum-vektor tér irányú vetületét:
A tapasztalat szerint az elektronnak pályamenti mozgásából adódó
momentumain kívül egy másik "saját" mágneses- és impulzusmomentuma is van.
Ezt nevezik spinnek, melyhez semmiféle klasszikus képet nem rendelhetünk. A
spinmomentumok: 
,
ill. 
, ahol s az
ún. spinkvantumszám.
Az atompályákat az elektronok az ún. felépítési elv szerint töltik be. A következő elektron mindig arra a pályára lép be, melyen a keletkezett atom energetikailag a legstabilabb lesz. Így pl. a 3p pályák teljes betöltése után a következő elektron nem a 3d, hanem a 4s pályát kezdi betölteni.
Molekulák az atomokból kémiai kötések segítségével jönnek létre. A kötések kialakulását, elrendeződését, a képződő molekulák szerkezetét és geometriáját különböző – kvantumkémiai elveken nyugvó – modelleken szemléltethetjük. Hangsúlyozzuk azonban, hogy e modellek a kvantummechanika törvényeinek csak részben tesznek eleget, a valóságot csak közelítik. Érdemük elsősorban szemléletességükben rejlik.
A molekulapályákat úgy képzeljük el, hogy azok atompályákból épülnek fel. Ennek megfelelően a molekulapálya (MO) az a térrész, melyben az elektron (ill. maximálisan két ellentétes spinű elektron) 90% valószínűséggel megtalálható. Lokalizált egy MO, ha mindössze két atomra terjed ki. Ilyen az egyszerű s kötés, mely akkor jön létre, ha a kötésben résztvevő két atompálya (AO) orientációja kötéstengely irányú. Erre adnak példát a XII.1. ábra rajzai. p kötés jön létre akkor, ha a pályák orientációi a kötéstengelyre merőlegesek. Nyilvánvaló az atompályák geometriáinak ismeretében, hogy p kötés s pálya részvételével nem jöhet létre. A lehetőségeket a XII.2. ábra szemlélteti.
Fontos megjegyezni, hogy atomok közötti első kötés mindig s , a további kettő pedig p típusú. Ez alól csak igen ritkán vannak kivételek. Mivel két atom között négy vagy több kötés ritkán alakul ki, d kötést eddig csak néhány fémkomplexben írtak le. Két AO-ból mindig két MO jön létre. Az egyik MO energiája mindig kisebb a kiindulási atompályák energiáinál, azaz a molekulát az ezen levő elektronok stabilizálják. Ezért az ilyen típusú pályát kötő molekulapályának nevezik. A másik MO energiája magasabb, mint a kiindulási atompályáké, így a molekulát a rajta levő elektronok destabilizálják. Az ilyen pályát lazító pályának nevezzük.
(s-s) (s-pz) (pz-pz)
(s-dz2) (p-dz2)
XII.1. ábra
(dxz-dxz) (px-px) (px-dxz)
XII.2. ábra
Molekulák geometriáját alapvetően mindig a s kötések határozzák meg, a p kötések csupán kis mértékben befolyásolják. Természetesen a rendszer minimális potenciális energiájú állapotának, azaz az egyensúlyi geometriának a kiszámítása nagyon bonyolult, így néhány egyszerű és szemléletes módszert dolgoztak ki a molekulageometria közelítő becslésére. Ilyen a vegyérték-elektronpár taszítási elmélet és a hibridizációs modell is.
A vegyértékhéjban levő elektronpárok olyan elrendeződést vesznek fel, mely maximálissá teszi az egymástól való távolságot. Tehát:
2 vegyérték-elektronpár: |
lineáris elrendeződés |
3 vegyérték-elektronpár: |
planáris trigonális |
4 vegyérték-elektronpár: |
tetraéderes |
6 vegyérték-elektronpár: |
oktaéderes |
A maximális távolságban levő elektronpárokat legegyszerűbben egy gömbmodellen képzelhetjük el, melynek középpontjában a központi atom, a gömb felületén pedig – egymástól a lehető legnagyobb távolságban – az egyes elektronpárok foglalnak helyet. E modell segítségével könnyen belátható, hogy a fentiektől eltérő számú vegyérték-elektronpár esetén a térbeli elhelyezkedés nem egyértelmű: az egyes formák között nem választhatunk teljes határozottsággal. Így pl. 5 vegyérték-elektronpár esetén két, nagyjából egyenértékű alakzat jöhet létre (XII.3. ábra), 7 elektronpár esetén 3 stb.
XII.3. ábra
Finomabb hatásokat vehetünk figyelembe a következő egyszerű szabályok segítségével.
A hibridizáció: atompályák lineáris kombinációja.
Hibridizáció során az eredeti atompályákból új, kötésirányú pályákat képezünk matematikai műveletek segítségével. Az új hibridpályák fizikai szempontból éppoly "szabályosak", helyesek, mint az eredeti AO-k, csupán – éppen orientációjuk miatt - sokkal szemléletesebbek. Orientációjuk következménye az is, hogy hibridpályák mindig csak s kötésekben fordulhatnak elő. A legfontosabb hibridizáció típusok és a hibridpályák által adott geometriák a következők:
sp |
lineáris |
sp2 |
planáris trigonális |
sp3 |
tetraéderes |
sp3d |
trigonális bipiramis |
sp3d2 |
oktaéderes |
Természetesen e néhány alapeseten kívül végtelen sok egyéb típus is lehetséges. Így pl. s és p pályákból képezett hibridtípusok jelentik a XII.4. ábra minden egyes pontját. Az ábra magyarázatot ad a kötésszög és a hibridizáció típusa közötti kapcsolatra is. A vegyérték-elektronpár taszítási elmélet szabályai nagyon egyszerűen összhangba hozhatók a hibridizáció szabályaival. Pl. a magányos elektronpár s karaktere mindig nagyobb, mint a kötőpároké. Ebből következik a nagyobb térigény (XII.4. ábra). Vagy pl. az elektronegatív ligandum a kötés p karakterét növeli. A további négy szabály változatlan. A hibridpályák előállítási szabályai a következők:
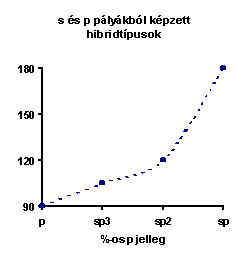
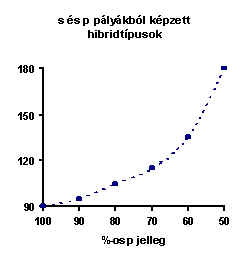
Ezek szerint a molekulák "felépítése" a következőképpen történik (pl. ICl3 molekula):
A benzol szabályos hatszög alakú planáris molekula. Mind a hat szénatomnak van a molekula síkjára merőleges állású p pályája, melyek p kötésekre képesek. Elképzelhető tehát 3 db lokalizált p kötés (Kekulé forma), de az is elképzelhető, hogy a 6 pálya együttesen alkot egy p rendszert. A tapasztalat az utóbbit igazolja. Az ilyen típusú kötésrendszert – mivel nincs két atomra lokalizálva – delokalizált kötésnek nevezzük. Ugyanúgy, ahogy a lokalizált kötések esetén két AO-ból két MO képződik, delokalizáció esetén n AO-ból n MO lesz. Természetesen a Pauli-elv itt is érvényes, egy MO-n két, ellentétes spinű elektron fér el.
Ismételten aláhúzzuk, hogy más, hasonló rendszereknél sem lehet pusztán logikai úton megállapítani, hogy egy kötés lokalizált vagy nem. Erre csak a kísérleti tapasztalat vagy pontos kvantumkémiai számítások nyújthatnak felvilágosítást.
