
IX. KÉMIAI EGYENSÚLY
Önként végbemenő folyamatok és egyensúly
A termodinamikai egyensúlyi állandó
Önként végbemenő folyamatok és egyensúly
Figyeljünk meg egy magára hagyott rendszert és vizsgáljuk meg, hogy milyen folyamatok mennek végbe önként (spontán). Egy folyamatot akkor nevezünk spontánnak, ha az külső behatás nélkül játszódik le. Például egy pohár forró víz az asztalra helyezve lehűl, csökkentve a víz és a szobahőmérséklet közötti hőmérsékletkülönbséget. Az ellenkező folyamat sohasem játszódik le, vagyis az, hogy a környezetével azonos hőmérsékletű víz magától (spontán) felmelegszik. Nyilvánvalóan az ellenkező irányú változást számtalan módon végre tudjuk hajtani pl. egy villamos árammal működő főzőlap segítségével, de ez csakis akkor játszódhat le, ha "hajtóerőt" alkalmazunk. A spontán folyamat hajtóereje a hőmérsékletkülönbség.
Megfigyelhetünk olyan folyamatokat, ahol nyomáskülönbség egyenlítődik ki. A gázok maguktól (spontán) kiterjednek, és az egész tartály térfogatát betöltik. Az ellenkező folyamat, mikor is a gáz (vagy gázelegy egy komponense) a palack egyik részébe gyűlik, magától sohasem megy végbe. Képesek vagyunk viszont egy gázt kisebb térfogatba sűríteni egy dugattyú segítségével. A spontán folyamat hajtóereje ez esetben a nyomáskülönbség.
Egy labda le tud gurulni a hegyről, de magától sohasem gurul vissza, a sajt a fára nem esik fel. Ebben az esetben a hajtóerő a két helyzet közötti potenciális energia különbség.
Ha fémnátrium darabkát vízbe dobunk, azonnal kémiai reakció játszódik le, amelynek során hidrogéngáz és nátrium-hidroxid keletkezik. Egy acéltárgy, ha néhány napig, vagy hétig szabad levegő és nedvesség hatásának van kitéve, megrozsdásodik. Ahhoz, hogy az említett két reakció ellenkező irányba játszódjék le, külső hatás szükséges. A kiindulási anyagok és a reakció termékei közötti hajtóerő a kémiai potenciál.
A fenti példákból és ezekhez hasonlókból az alábbi közös következtetéseket vonhatjuk le.
Mi a közös tehát a tárgyalt folyamatokban? Milyen termodinamikai elv ad magyarázatot arra, hogy adott körülmények között egy folyamat egy bizonyos irányba játszódik le és nem az ellenkezőbe?
A termodinamikában egy állapotfüggvényt, az entrópiát (jele: S) definiáltak a spontán folyamatok lejátszódásának jellemzésére: minden önként lejátszódó változás a világegyetem entrópiájának növekedésével jár együtt. Ez a termodinamika második főtétele. (Emlékeztetoül az első főtétel: A világegyetem energiája állandó.) Figyelmünket egy jól definiált rendszerre korlátozva ugyanez a törvényszerűség állapítható meg. Egy elszigetelt rendszer entrópiája mindig nő a folyamat során és akkor éri el maximumát, ha már makroszkopikus változás nem történhet, azaz egyensúlyban van (S = max).
Nyilvánvalóan az S változásának ki kell terjednie arra a környezetre is, amelyre a folyamat hat. Így nemcsak a lehűlő pohár víz entrópiája változik, hanem a környező levegő, az asztal, a laboratórium és végső soron az egész világegyetem entrópiája is.
DSösszes = DSrendszer + DSkörnyezet
Ha egy adott folyamatra nézve DSösszes pozitív érték, akkor a folyamat magától játszódik le, azaz spontán. Amennyiben DSösszes értéke negatív, akkor a folyamat az ellenkező irányba játszódik le.
Nagyon sok esetben a DSkörnyezet értéke nem számítható ki. Ezért az önként lejátszódó változások mértékéül az entrópia helyett egy másik termodinamikai tulajdonság, a Gibbs-féle szabadentalpia kifejezését használják gyakrabban, amelynek definíciója:
G = H - TS (1)
állandó nyomás és hőmérséklet esetében pedig:
Mivel zárt rendszerben magától lejátszódó folyamat feltétele az, hogy DS > 0, izoterm és izobár folyamat esetében az önként végbemenő folyamat a szabadentalpia csökkenésével jár együtt, azaz DG < 0. Nyilvánvaló, a DG értékét a (2) egyenlet szerint DH és TDS különbsége határozza meg, így mindkét tényező nagyságát meg kell vizsgálni. Könnyen levonhatjuk azt a következtetést, hogy negatív DH és pozitív DS kedvez a spontán változásoknak, mivel az ilyen jellegű folyamat DG negatív értékét jelzi. Megfordítva, endoterm változás (DH > 0) negatív entrópia változással semmilyen hőmérsékleten sem játszódhat le magától. Mégis, endoterm folyamat lehet spontán, ill. nem spontán, az entrópiaváltozás értékétől függően. Összesen a DH és DS értékétől függően 4 lehetséges alapeset van, melyek a következők:
Eset |
DH |
DS |
T |
DG |
Eredmény |
példa |
1 |
- |
+ |
- |
spontán |
2H2(g)+O2(g) => 2H2O(g) |
|
2 |
- |
- |
alacsony | - | spontán |
H2O(f) => H2O(sz) |
| magas | + |
nem spontán |
||||
+ |
+ |
alacsony | + |
nem spontán |
2NH3(g) => N2(g) + 3H2(g) |
|
| magas | - |
spontán |
||||
4 |
+ |
- |
+ |
nem spontán |
3O2(g) => 2O3(g) |
Mint az fenti táblázatból látható, a 2. és a 3. alapeset nem egyértemű, 2 további lehetőséget tatalmaz. Példaképpen vizsgáljuk meg a 3. esetet, mikor is mind DH, mind DS értéke pozitív. A IX.1. ábrán az egyik függvény az entalpia változását mutatja be a hőmérséklet függvényében, a másik pedig a TDS szorzatát szintén a hőmérséklet függvényében.

1. ábra
A DH rendszerint nem nagyon érzékeny a hőmérsékletváltozásra, így a függvény meredeksége általában kicsi. A TDS függvény meredeksége várhatóan nagy a hőmérsékleti tényező jelenléte miatt. A függőleges vonalak DG értékét adják meg. Az ábra bal oldalától indulva DG értéke csökken T növelésével. Az ábra jobb oldalán TDS értéke meghaladja DH értékét, így DG negatívvá válik. A két görbe kereszteződésében DG = 0, a rendszer egyensúlyban van. Nézzük meg azt a folyamatot, amikor a jég vízzé olvad:
H2O(sz) -> H2O(f)
Ez a folyamat endoterm és DS is pozitív, így a magától lejátszódó folyamat iránya a hőmérséklettől függ. Alacsony hőmérsékleten DH dominál és a reakció magától visszafelé játszódik le, a víz megfagy. Magasabb hőmérsékleten DS értéke meghaladja DH értékét; a jég megolvad. Egy különleges T értéknél (olvadáspont) DH = TDS, ekkor víz és jég együtt létezhetnek.
A leírtakat összegezve DG-t egy (nem szükségszerűen kémiai) folyamat hajtóerejének tekinthetjük. A negatív előjelű DG egy reakció spontán lejátszódásának termodinamikai feltétele. Ez a feltétel azonban semmit sem mond a folyamat kinetikájáról. Negatív előjelű DG-vel rendelkező folyamat olyan lassan is végbemehet , hogy emberi észlelés számára szinte észrevehetetlen.
Normál szabadentalpia változásról (DGo) olyankor beszélünk, amikor egy folyamat valamennyi résztvevője normál állapotban van. (A hőmérséklet 25 oC, a nyomás értéke 101325 Pa, az anyagok tiszta folyadék, ill. tiszta szilárd állapotban vannak jelen, a gázokat a tökéletes gáz állapot jellemzi, oldatok esetében a koncentráció az oldott anyagra nézve 1 M és az elegy ideális.) DGo tehát egy olyan reakció szabadentalpiaváltozása, melynek során a normál állapotú kiindulási anyagok (reakció-partnerek) normál állapotban lévő termékekké alakulnak.
Egy anyag képződési szabadentalpiája, DG0k az a szabadentalpiaváltozás, amely 1 mol anyag alkotóelemeiből való képződését kíséri minden reakció- és végterméket normál állapotban véve (v.ö a DH0k fogalmával).
Egy reakció normál szabadentalpiáját DG0k-kból számíthatjuk:
![]() (3)
(3)
Azaz DGo -t megkapjuk, ha a termékek (t) DG0k összegébol levonjuk a reagáló anyagok (r) DG0k összegét. Az eljárás azonos egy reakció DH entalpiaváltozásának számításával.
Számítások céljára néhány DG0k értéket a Függelék 14. táblázatában gyűjtöttük össze.
Egy reakció hajtóereje, de még az iránya is a hőmérséklettől, a nyomástól és a reakcióba lépő, ill. a keletkező anyagok koncentrációjától függ. Az összefüggés - részletes tárgyalástól eltekintve - az alábbi képlettel adható meg:
DG = DGo + RT . lnQ (4)
ahol a hőmérséklettől való függés nyilvánvaló. A nyomás- és koncentrációfüggés a Q reakció- hányadosban van elrejtve. A fenti "reakcióhányados" olyan kifejezés, ami az adott rendszer minden összetevőjének pillanatnyi koncentrációját tartalmazza:
A végtermékek koncentrációinak szorzatát el kell osztani a reakcióba lépő anyagok koncentrációinak szorzatával. (Terméknek nevezzük a reakcióegyenlet jobb oldalán lévő anyagokat, reakcióba lépő anyagoknak a bal oldalon lévőket.)
Mindegyik koncentrációt annyiadik hatványra kell emelni, amennyi a rendezett egyenletben a megfelelő anyag együtthatója. Így az alábbi egyenlet esetében
n A + m B = k C + l D (5)
Q értéke:
![]() (6)
(6)
ahol a szögletes zárójelek a molaritást jelentik. Szigorú értelemben a reakcióhányadost nem koncentráció értékekkel, hanem az ún. aktivitásokkal kell számítani.
 (7)
(7)
Az aktivitás a koncentrációtól függ, a = f(x), és a standard állapotra vonatkozik:
Tiszta szilárd anyagokra és folyadékokra az aktivitást egységnyinek tekintjük, a = 1. Korlátlanul elegyedő anyagok esetében:
lim a = x
x -> 1
lim a = x
x -> 0
lim a = ![]()
p -> 0
ahol x a moltört, pa a parciális nyomás, po = 101325 Pa.
Az aktivitás minden elegyben mindegyik anyag egyedi függvénye. Rendszerint azonban az aktuális aktivitási értékek ismeretlenek. Ezekben az esetekben fel kell tételeznünk azt, hogy az aktivitás a megfelelő koncentrációval egyenlő. Ebben a fejezetben minden esetben figyelmen kívül fogjuk hagyni az aktivitásokat és koncentrációkkal vagy (gázok esetében) parciális nyomásokkal fogunk számolni.
Az előző pontban megállapítottuk, hogy a rendszerben olyan
folyamatok játszódhatnak le önként, amelyek a rendszer szabadentalpiáját
csökkentik. Egy rendszerben, melyben kémiai reakció megy végbe, a koncentráció, ill.
a nyomás úgy változik meg, hogy a rendszer összes szabadentalpiája a minimumot érje
el. A IX.2. ábrán a szabadentalpiát a reakció
előrehaladásának függvényében ábrázoltuk. A termékek és a reagáló anyagok
standard moláris szabadentalpiájának különbsége ![]() .
.
Az egyensúlyi pont valahol a tiszta végtermékek és a kiinduló anyagok között helyezkedik el. Az egyensúlyi elegy szabadentalpiája kisebb, mint bármely ettol eltéro elegyé. így bármely más elegyben olyan változás megy végbe, ami az egyensúly felé mutat.
Egyensúlyban DG = 0. Ha a Q reakcióhányados kifejezésbe az egyensúlyi értékeket helyettesítjük, a kifejezést tömeghatás-törtnek, értékét pedig egyensúlyi állandónak nevezzük és "K"-val jelöljük:
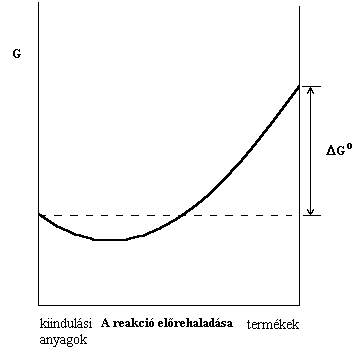
2. ábra
Ha ![]() pozitív, vagy
kis negatív érték, az egyensúlyi elegy mind a kiindulási, mind a végtermékekből
jelentős mennyiséget tartalmaz. Ha
pozitív, vagy
kis negatív érték, az egyensúlyi elegy mind a kiindulási, mind a végtermékekből
jelentős mennyiséget tartalmaz. Ha ![]() =
0, ez azt jelenti, hogy K = 1.
=
0, ez azt jelenti, hogy K = 1.
Ha ![]() nagy pozitív
érték, a szabadentalpia minimuma a tiszta kiindulási anyagok oldalához esik igen
közel és az egyensúlyi pont eléréséig a reakció csak kis mértékben megy végbe.
Ebben az esetben K értéke egynél kisebb lesz. Az alábbi reakció esetében
nagy pozitív
érték, a szabadentalpia minimuma a tiszta kiindulási anyagok oldalához esik igen
közel és az egyensúlyi pont eléréséig a reakció csak kis mértékben megy végbe.
Ebben az esetben K értéke egynél kisebb lesz. Az alábbi reakció esetében
C(sz) + H2O(g) Ű CO(g) + H2(g)
K = 1,6× 21-21 25 oC-on, ami azt jelenti, hogy szobahőmérsékleten alig játszódik le reakció.
Ha ![]() nagy negatív
érték, a szabadentalpia minimuma a végtermék oldalhoz esik nagyon közel és a
reakció lényegében teljesen végbemegy. Ebben az esetben K értéke nagy. Így az
alábbi reakcióra
nagy negatív
érték, a szabadentalpia minimuma a végtermék oldalhoz esik nagyon közel és a
reakció lényegében teljesen végbemegy. Ebben az esetben K értéke nagy. Így az
alábbi reakcióra
2 H2(g) + O2(g) Ű 2 H2O(f)
K = 1,4× 1083 25 oC-on, ezért a reakció gyakorlatilag teljesen végbemegy.
Az egyensúlyi állandó számításánál használt koncentrációk oldatok esetében többnyire molkoncentrációk (Kc), korlátlanul elegyedő rendszerekre pedig moltört értékek (Kx).
Ha a komponensek gázok, a koncentrációk parciális nyomásokkal (Kp), vagy a molok számával is (Kn) kifejezhetők. Ezért a feltételezett (5) reakció esetében az egyensúlyi állandók a következők:
Kc = ![]() ;
; 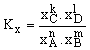 ;
;  ;
; ![]() (9)
(9)
Az aktivitás fogalma miatt pi (Pascalban adva) helyett Kp számításánál a pi/po mennyiségeket használjuk, ahol po = 101325 Pa. A különböző egyensúlyi állandók között könnyen lehet összefüggést találni. Mivel
pi = xipö (Dalton törvénye) és pi/po = xi pö/po, ezért
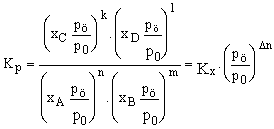 (10)
(10)
ahol Dn = k + l - n - m
A Kp és Kc között az összefüggés a tökéletes gázokra vonatkozó gáztörvényből fejezhető ki;
pi .Vössz = ni.RT (11)
Egy adott "A" komponens molaritása;
[A] =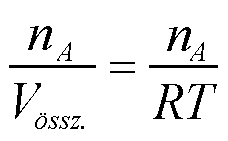 (12)
(12)
Az (5) egyenletre felírható egyensúlyi állandó:
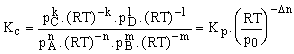 (13)
(13)
(10)-ből és (13)-ból
Kx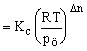 (14)
(14)
Mivel ![]() (a moltört definíciója);
(a moltört definíciója);
Kx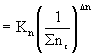 (15)
(15)
a (10) és (15) kifejezésből

Egy adott egyensúlyi állandó szigorúan egy adott reakcióegyenlethez rendelhető. A 17. feladat alapján az alábbi következtetések vonhatók le:
Tételezzük fel, hogy a következő reakciók egyensúlyi állandóit (K1 és K2) ismerjük:
és a következő reakció K3 értékét szeretnénk tudni:
A c. reakcióegyenletet a. és b. egyenletekből kaphatjuk meg: c = a + b. Szorozzuk össze a két egyensúlyi állandót, K1-t, valamint K2-t és a hozzájuk tartozó kifejezéseket.
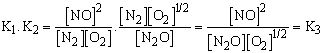
E példa alapján alkotható a negyedik szabály:
Különleges gázreakció a termikus disszociáció, amikor egy molekula bomlásakor kettő, vagy több molekula keletkezik. Ilyen reakciók jellemzésére a disszociációfok, a fogalmát használják, amely az elbomlott vegyület hányadát fejezi ki:
![]()
Némely esetben a reagáló anyagok eltérő fázisokban vannak jelen és a reakció a szilárd anyag, ill. a folyadék felületén megy végbe. Ha az egyik komponens tiszta anyag és koncentrációja nem változik (csak rendkívül kismértékben változik) meg a reakció során, az az egyensúlyi állandó kifejezéséből kizárható.
A víz képes önmagával reagálni, amelynek folyamán hidroxónium (H3O+) és hidroxid (OH-) ionok keletkeznek:
H2O + H2O Ű H3O+ + OH-
Ennek a reakciónak az egyensúlyi állandója:

Mivel Kc igen kis érték, ez azt jelzi, hogy a víz koncentrációja a reakció során nem változik (alig változik). A víz koncentrációját állandónak tekinthetjük és az alábbi kifejezést a víz ionszorzatának nevezzük:
Kv = [H3O+] . [OH-] (17)
Kv számértéke 25 oC-on 1× 10-14 (mol/dm3)2,. így a tiszta vízben az ionkoncentráció
[H3O+] = [OH-] = 1.10-7 mol/dm3
A víz szerkezete valójában bonyolult. Nemcsak H3O+ és OH- ionok vannak benne, hanem más ionok létezését is kimutatták. Ezért az egyszerűség kedvéért Kv kifejezését gyakran egyszerűbb alakban használjuk, ami mellesleg nem okoz változást a továbbiakban:
Kv = [H+][OH-] (18)
ahol a H+ kifejezés az összes hidratált protont reprezentálja. A [H3O+], (vagy [H+]) ionkoncentráció nagy jelentőséggel bíró fogalom. Minden biokémiai reakciót és számos vegyipari folyamatot a [H3O+] értékének mérésével ellenőriznek. Mivel többnyire kényelmetlen kis hatványértékeket használni, bevezették a pH fogalmát.
A pH kifejezés a mol/dm3 értékben vett H+ ionkoncentráció tizes alapú logaritmusának negatív előjellel vett értéke. Így 25 oC-on egy semleges oldat pH-ja:
[H3O+] = [OH-] = 1.10-7 mol/dm3 pH = -lg [H3O+] = 7
A pOH értéket hasonló módon, mint -log[OH-]-t definiáljuk.
Ha vízhez valamilyen savat adunk, a sav szintén ionizálódik
(disszociál) H3O+ ionokat képezve. Ezek az ionok
természetesen szintén jelentkeznek a víz ionszorzatában és az összes H3O+
koncentráció adja a vizes oldat pH-ját. Erős savak disszociációja H3O+
ionokra majdnem teljes, és hacsak az oldat nem túlzottan híg, a sav
disszociációjából származó ![]() érték néhány nagyságrenddel nagyobb, mint ami a víz
disszocációjából származik. Fenti meggondolás miatt többnyire elfogadott dolog az,
hogy csak az erős sav disszocációjából származó H3O+-t
vesszük figyelembe. Hasonló meggondolások érvényesek erős bázisokra.
érték néhány nagyságrenddel nagyobb, mint ami a víz
disszocációjából származik. Fenti meggondolás miatt többnyire elfogadott dolog az,
hogy csak az erős sav disszocációjából származó H3O+-t
vesszük figyelembe. Hasonló meggondolások érvényesek erős bázisokra.
Gyenge savak és bázisok (Kc«1) vizes oldatának a disszociációja nem teljes. Vízben disszociálnak és egyensúlyi elegy jön létre, amely a molekulákat és a belőlük származó ionokat tartalmazza. A közös H3O+ ionoknak a víz ionszorzatában, valamint a gyenge savak-bázisok egyensúlyában is szerepe van. Ezért a feladatok megoldása bonyolultabb, mint a gázegyensúlyoké. Talán a legfontosabb lépés a feladatok megoldása során annak a problémának meghatározása, hogy egyensúly esetén mely komponens az, amelyik meghatározóan fontos és mely hanyagolható el. Ezt már a 45. példa esetében a számítások különbözo szintjein bemutattuk és a továbbiak során is példákon keresztül fogjuk szemléltetni.
Megjegyezzük, hogy a disszociáció és ionizáció kifejezést egyaránt alkalmazzák, mert savak és bázisok disszociálnak és ionizálódnak egyidejűleg. Mégis a protonátvitel (ionképződés) a lényeges lépés ezekben a reakciókban. A szakirodalomban gyenge savak és bázisok egyensúlyi állandóját Ka-val, ill. Kb-val (magyar nyelvű irodalomban a savállandót gyakran Ks-sel) jelölik. Tárgyalásaink során, amennyiben nem zavaró, az általánosabb Kc jelölést fogjuk alkalmazni. A különbözo gyenge savak és bázisok Kc értékeit a 15. táblázatban foglaltuk össze.
Azokat a savakat, amelyek egynél több protont képesek leadni, több
bázisú savaknak nevezzük. Egyszerű példák erre a kétbázisú H2S, H2SO4,
H2CO3 vagy a hárombázisú foszforsav, a H3PO4.
Többsavú bázisok több mint egy protont tudnak felvenni, példa erre a Ca(OH)2.
Szeretnénk felhívni a figyelmet arra, hogy a Brönsted-elmélet szerint a protonleadás
és a protonfelvétel dinamikus folyamatok: ha egy sav protont ad át (donál) a víznek,
a keletkező savion új bázissá válik (az eredeti sav konjugált bázisává), mert H3O+
iontól protont képes felvenni, amelyik viszont a H2O "bázis"
konjugált sava. Ezért többsavú bázis a ![]() és több bázisú sav a Ca2+ ion.
és több bázisú sav a Ca2+ ion.
Több bázisú savak és többsavú bázisok egyensúlyai az átadott, ill. felvett protonok számának megfelelő számú egyensúlyi állandó segítségével írhatók le.
A következő kétbázisú savra két szimultán egyensúlyt lehet figyelembe venni.
| H2A + H2O Ű HA- + H3O+ | 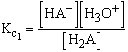 |
| HA- + H2O Ű A2- + H3O+ | |
| Az egyensúlyi állandó a teljes disszociációra: | |
| H2A + 2 H2O Ű A2- + 2 H3O+ | 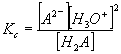 |
ahol ![]()
Néhány általános szabályt lehet rögzíteni.
A 66. feladat megoldása során látszik, hogy a nátrium-acetát oldat lúgos kémhatású, pH > 7,00. Egy sóoldat savas, vagy lúgos kémhatása előre megítélhető az ionok oldatban való viselkedéséből. Ha egy só vízzel kémiai reakcióba lép, ezt a folyamatot hidrolízisnek nevezzük. A megfelelő egyensúlyi állandót pedig hidrolízis állandónak nevezzük.
Az ecetsav disszociációja során ugyanúgy, mint a nátrium-acetát disszociációjakor acetátionok képzodnek . A só azonban erős elektrolit és teljes mértékben disszociál, így a közös ionok igen nagy része a sóból származik. A disszociációs egyensúlyban az összes acetátion részt vesz, tekintet nélkül arra, hogy honnan származik. Az acetátion nagy koncentrációja miatt a H3O+ koncentráció az elegyben kisebb lesz, mint a tiszta sav oldatban, mert az anion a gyenge sav disszociációját visszaszorítja. Ilyen esetben az alábbi közelítést lehet alkalmazni; az egyensúlyi elegyben az anion koncentráció egyenlő a só koncentrációval és a nem disszociált sav koncentrációja megegyezik a kiindulási sav koncentrációjával. Nyilvánvaló az, hogy hasonló következtetést lehet levonni gyenge bázis és annak sója esetében. Az ilyen oldatokat puffer oldatoknak nevezzük. A puffer oldatok lényege és jellemző tulajdonsága az, hogy ellenállnak a pH érték megváltozásának, ha H3O+ vagy OH- ionok nagyobb koncentrációja éri őket, azaz savak vagy bázisok hozzáadása esetén is (lásd 75. és 76. feladatot).
Hasonló közös ion hatás észlelhető, ha erős savat öntünk gyenge sav oldatába, vagy ha erős bázist elegyítünk gyenge bázis oldatával. Ezekben az esetekben a H3O+ vagy az OH- ion koncentráció az erős savtól (bázistól) függ, a gyenge sav (bázis) disszociációja visszaszorul.
Egy só telített oldatában az oldott anyag és a fel nem oldott anyag egyensúlyban vannak, amit a következő egyensúlyi állandó fejez ki:

Ez az egyensúlyi állandó formális, mivel az egyensúly a szilárd anyag mennyiségétol vagy koncentrációjától független, amennyiben az oldat telített. (Ld. heterogén egyensúlyok.) A feloldódott só azonban teljesen disszociál, ezért a fenti egyensúlyi kifejezést a disszociációs reakcióval lehet kombinálni. Egy sóra, amely disszociációkor m darab M kationt és n darab X aniont ad, felírható:
Mm . Xn = mM + nX
Behelyettesítve az egyensúlyi kifejezésbe:
K = [M]m . [X]n
Az oldhatósági állandó ezen típusát oldhatósági szorzatnak nevezzük.
Bár a kifejezésben használt koncentrációk molokban szerepelnek, így a Kc jelölést alkalmazhatnánk, mégis a szakirodalomban az "L" vagy Ksp jelölést használják. Az oldhatóság függ a hőmérséklettől, saját és idegen ionoktól, a pH-tól és a komplexképződéstől.
Az oldhatósági szorzatot meg kell különböztetni az oldhatóságtól (s), az oldhatósági szorzat mol/dm3-ben megadott egyensúlyi helyzetet jellemez.